जादूगर से पूछो #405
x 2 - 3 = sqrt(x+3). x का मान ज्ञात कीजिए।
मान लीजिए y = दोनों व्यंजक। तो, हमारे पास है:
- y = x^2 - 3
- y = sqrt(x+3)
दोनों व्यंजकों में 3 पर ध्यान दें। आइए दोनों समीकरणों को एक तरफ 3 रखकर व्यक्त करें। सबसे पहले हमारे पास है:
3 = x^2 - y
अब, आइए ऊपर दिए गए दूसरे समीकरण का वर्ग करें:
y^2 = x+3
3 = y^2 - x
आइए 3 के लिए दोनों अभिव्यक्तियों को समान मानें:
x^2 - y = y^2 - x
आइये पुनः व्यवस्थित करें:
x^2 - y^2 + x - y = 0
(x+y)(xy) + x - y = 0
(xy)(x+y+1) = 0
सबसे पहले आइए xy = 0 की जांच करें:
xy = 0
आइए y के स्थान पर y = x^2 - 3 प्रतिस्थापित करें।
एक्स - (x^2 - 3) = 0
x^2 - x - 3 = 0
पाइथागोरस सूत्र का उपयोग करते हुए:
x = (1 +/- sqrt(1 + 12)/2
x = (1 + sqrt(13)/2 और x = (1 - sqrt(13)/2
दूसरा, आइए x+y+1 = 0 की जांच करें:
आइए y के स्थान पर y = x^2 - 3 प्रतिस्थापित करें।
एक्स + (x^2 - 3) + 1 = 0
x + x^2 - 3 + 1 = 0
x^2 + x - 2 = 0
पाइथागोरस सूत्र का उपयोग करते हुए:
x = (-1 +/- sqrt(1 + 8)/2
x = (-1 +/- 3)/2
x = 1, x = -2
तो, हमारे चार उत्तर हैं:
- एक्स = 1
- एक्स = -2
- x = (1 + sqrt(13)/2 =~ 2.302776
- x = (1 - sqrt(13)/2 =~ -1.302776
मैं इस समस्या को हल करने की विधि के लिए SyberMath द्वारा YouTube वीडियो Solving x^2-3=sqrt(x+3) का धन्यवाद करना चाहूँगा। इस विधि के लिए 6:28 बिंदु पर जाएँ।
त्रिज्या 1 वाले वृत्त के बाहर स्थित एक बिंदु परिधि का 1/3 भाग देख सकता है। बिंदु कितनी दूरी पर है?
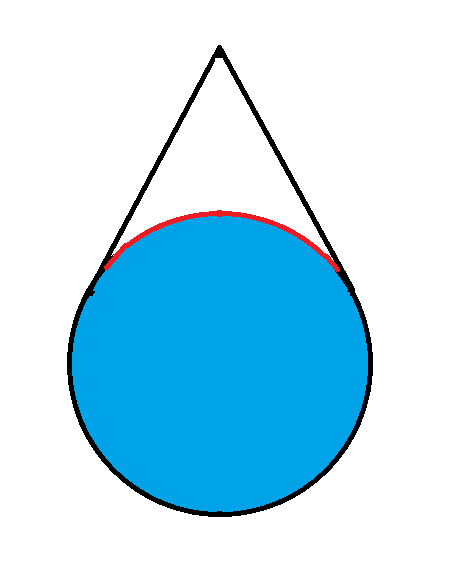
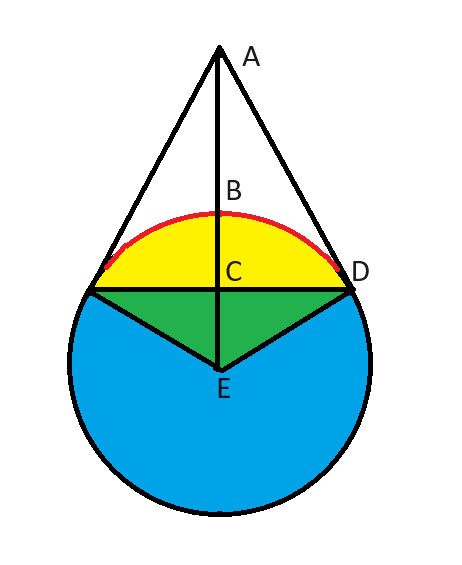
त्रिभुज ADE पर विचार करें। हम जानते हैं:
- कोण ADE 90 डिग्री है, क्योंकि AD वृत्त की स्पर्श रेखा है।
- कोण AED 60 डिग्री है, क्योंकि E पर हरे त्रिभुज का कोण 120 डिग्री (पूरे 360 का 1/3) है।
- कोण EAD त्रिभुज ADE के अन्य 30 अंश के बराबर होना चाहिए।
यह एक पारंपरिक 30-60-90 त्रिभुज है। हम सभी को पता होना चाहिए कि इस त्रिभुज की भुजाएँ 1, 2 और sqrt(3) के समानुपाती होती हैं।
इस स्थिति में ED = 1, जैसा कि प्रश्न में दिया गया है। AE उस दूरी का दोगुना है, अर्थात 2।
2, बिंदु से वृत्त के केंद्र तक की दूरी है। हमसे बिंदु से वृत्त पर स्थित निकटतम बिंदु तक की दूरी पूछी जाती है। इसलिए हम त्रिज्या घटा देते हैं। इस प्रकार, उत्तर 2-1 = 1 है।
बॉब और टॉम एक रेल पुल पर चल रहे हैं और अपने शुरुआती बिंदु से एक-तिहाई दूरी तय कर चुके हैं। तभी उन्हें पीछे से एक रेलगाड़ी आती हुई सुनाई देती है। दोनों 5 मील प्रति घंटे की रफ़्तार से दौड़ सकते हैं। बॉब पीछे मुड़ता है और टॉम आगे दौड़ता है। दोनों एक सेकंड से भी कम समय से रेलगाड़ी से चूक जाते हैं। रेलगाड़ी की गति कितनी थी?
याद रखें दूरी = गति * समय, जिसे हम d = r*t के रूप में व्यक्त करेंगे
इसे पुनः लिखते हुए: t = d/r.
पुल के आरंभ में बॉब और ट्रेन दोनों की मुलाकात का समय एक ही है:
आइये:
- x = ट्रेन के प्रारम्भिक भाग और पुल के प्रारम्भिक भाग के बीच की दूरी।
- r = ट्रेन की गति की दर
सबसे पहले, बॉब को देखते हैं, जो वापस दौड़ता है। आइए बॉब और ट्रेन दोनों के पुल के शुरू में मिलने के लिए t को व्यक्त करें:
बॉब: t = (1/3)/5
ट्रेन: t = x/r
t के लिए दो अभिव्यक्तियों को समान करना:
(1/3)/5 = x/rआर/3 = 5x
आर = 15x
दूसरा, आइए टॉम को देखें, जो आगे दौड़ रहा है। आइए टॉम और ट्रेन दोनों के पुल के शुरू में मिलने के लिए t को व्यक्त करें:
टॉम: t = (2/3)/5
ट्रेन: t = (1+x)/r
t के लिए दो अभिव्यक्तियों को समान करना:
(2/3)/5 = (1+x)/आर
2आर/3 = 5(1+x)
2आर = 15(1+x)
2r = 15 + 15x
इस समय हमारे पास है:
- आर = 15x
- 2r = 15 + 15x
आइए पहले समीकरण में r के लिए अभिव्यक्ति को दूसरे में प्रतिस्थापित करें:
30x = 15 + 15x
15x = 15
एक्स = 1
याद करें, r = 15x.
तो, ट्रेन की गति 15*1 = 15 मील प्रति घंटा है।


