जादूगर से पूछो #399
अगर आप पहली तस्वीर से छोटा वर्ग निकाल दें और टुकड़ों को फिर से व्यवस्थित करें, तो कुल क्षेत्रफल अभी भी वही लगता है। यह कैसे संभव है?
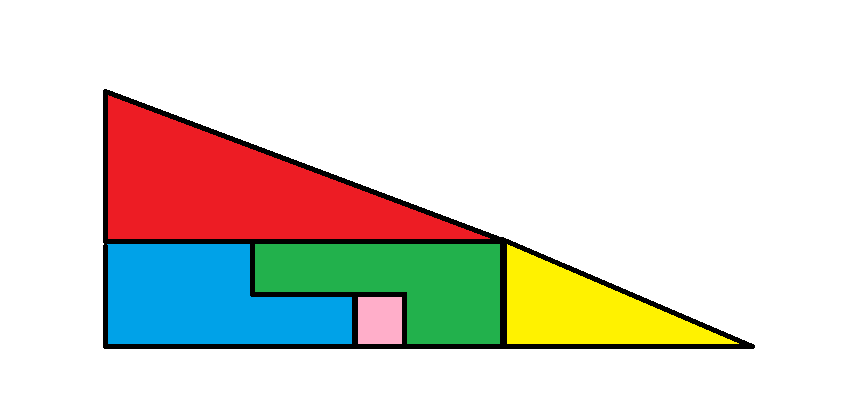
चित्र 1
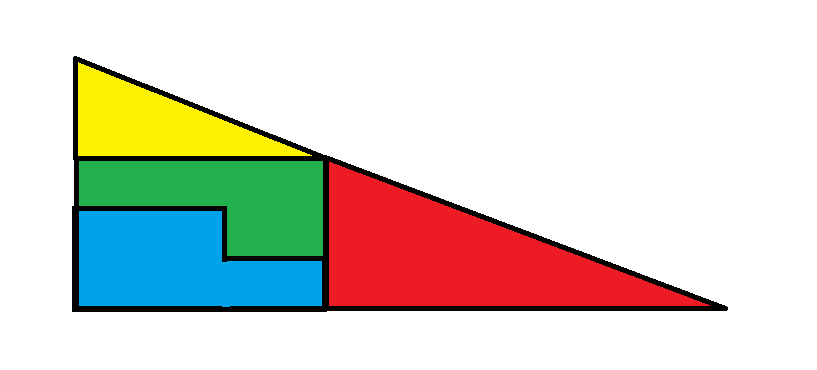
चित्र 2
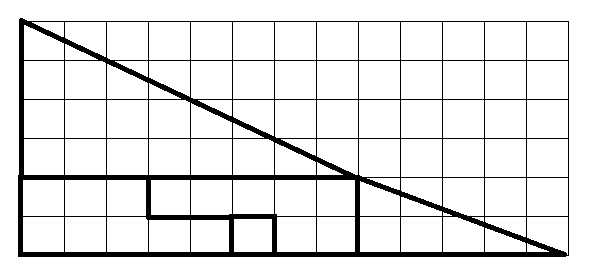
ऊपर दी गई छवि में पहली छवि को ग्रिड पर दिखाया गया है, ताकि प्रत्येक टुकड़े का आकार बेहतर ढंग से देखा जा सके।
ध्यान दें कि बड़े लाल त्रिभुज की भुजाएँ क्रमशः 4 और 8 हैं। इसके बाद, छोटे पीले त्रिभुज की भुजाएँ क्रमशः 2 और 5 हैं। दूसरे शब्दों में, ये त्रिभुज समानुपाती नहीं हैं। दोनों त्रिभुजों के कर्ण का ढलान दोनों आकृतियों में दिखाए गए समान नहीं है। एक का ढलान 0.5 है और दूसरे का 0.4। टुकड़ों को दोनों आकृतियों में जिस तरह रखा गया है, उससे ऐसा लगता है कि वे 5 और 13 भुजाओं वाला एक बड़ा त्रिभुज बनाते हैं, लेकिन यह त्रिभुज नहीं है।
लाल त्रिभुज का क्षेत्रफल 4*8/2 = 16 है।
पीले त्रिभुज का क्षेत्रफल 2*5/2 = 5 है।
पहली छवि में, अन्य तीन टुकड़े 2 गुणा 8 आकार का एक आयत बनाते हैं, जिसका कुल क्षेत्रफल 16 है।
दूसरी छवि में, अन्य दो टुकड़े 3 गुणा 5 आकार का एक आयत बनाते हैं, जिसका कुल क्षेत्रफल 15 है।
पहली छवि का कुल क्षेत्रफल लाल त्रिभुज + पीला त्रिभुज + बड़ा आयत = 16 + 5 + 16 = 37 है।
दूसरी छवि का कुल क्षेत्रफल लाल त्रिभुज + पीला त्रिभुज + छोटा आयत = 16 + 5 + 15 = 36 है।
निष्कर्ष यह है कि पहली छवि छोटे वर्ग के साथ बड़ी है। यह एक दृष्टिभ्रम है कि दोनों ही मामलों में कुल टुकड़े मिलकर एक बड़ा त्रिभुज बनाते हैं। ऐसा नहीं है।
एक विशाल रेगिस्तान के किनारे पर 16 मोटरसाइकिलें खड़ी हैं। हर मोटरसाइकिल एक टैंक पेट्रोल भरकर 100 मील का सफ़र तय कर सकती है। सभी मोटरसाइकिलें पूरी तरह से भरी हुई टैंक के साथ शुरू होती हैं। मोटरसाइकिलों के बीच पेट्रोल ट्रांसफ़र की अनुमति है। लक्ष्य एक मोटरसाइकिल को उसके शुरुआती बिंदु से जितना हो सके दूर ले जाना है। यह कितनी दूर जा सकती है?
समस्या की जड़ यह है कि समूह थोड़ी दूर तक जाए। फिर एक मोटरसाइकिल से बचा हुआ पेट्रोल निकाल लें और बाकी की टंकियों में ईंधन भर दें।
उदाहरण के लिए, शुरुआत में पेट्रोल से भरे एक टैंक को 16 भागों में बाँट लें, हर मोटरसाइकिल के लिए एक। फिर सभी लोग मिलकर तब तक गाड़ी चलाएँ जब तक टैंक का 1/16 हिस्सा खत्म न हो जाए, जिससे समूह को 100/16 = 6.25 मील की दूरी तय करनी होगी। एक मोटरसाइकिल से टैंक का 15/16 हिस्सा लें और बाकी 15 मोटरसाइकिलों में 1/16 हिस्सा डालें, जिससे उनमें ईंधन पूरी तरह भर जाएगा।
फिर यही प्रक्रिया दोहराएँ, लेकिन 15 मोटरसाइकिलें बची रहने पर, टैंक के 1/15 भाग जितनी दूरी तय कर सकें, उतनी दूरी तय करें, जो 100/15 = 6.666667 मील है। फिर एक मोटरसाइकिल से एक और 14/15 टैंक लें और बाकी 14 मोटरसाइकिलों में 1/15 टैंक भर दें।
इस प्रक्रिया को जारी रखने पर अंतिम मोटरसाइकिल को कुल दूरी (1/16) + (1/15) + (1/14) + ... + (1/1) =~ 338.072899 मील मिलेगी।
[/spoiler]यह प्रश्न विज़ार्ड ऑफ़ वेगास में मेरे मंच पर पूछा गया और इस पर चर्चा की गई।
स्लीपिंग ब्यूटी पैराडॉक्स पर आपके क्या विचार हैं?
अन्य पाठकों के लाभ के लिए, स्लीपिंग ब्यूटी समस्या/विरोधाभास में जो पूछा जा रहा है, वह यहां दिया गया है।
स्लीपिंग ब्यूटी (एसबी) एक प्रयोग के लिए स्वयंसेवा करती है। प्रयोग की पूरी जानकारी उसे सच्चाई के साथ इस प्रकार समझाई जाती है:
- रविवार: एसबी को सुला दिया जाएगा। उसके सो जाने के बाद एक निष्पक्ष सिक्का उछाला जाएगा।
- सोमवार: एसबी को सोमवार को जगाया जाएगा और पूछा जाएगा, "सिक्का चित पर आने की क्या सम्भावना है?" उसके उत्तर देने के बाद उसे पुनः भूलने की दवा देकर सुला दिया जाएगा, जिससे वह सोमवार को हुई सारी बातें भूल जाएगी।
- मंगलवार: अगर सिक्का पट पर गिरा, तो सोमवार को जो हुआ था वही फिर होगा। अगर सिक्का चित पर गिरा, तो वह पूरा दिन सोती रहेगी।
- बुधवार: एसबी को फिर से जगाया गया, उससे कुछ नहीं पूछा गया, तथा प्रयोग समाप्त होने पर वह घर चला गया।
सवाल यह है कि सोमवार और संभवतः मंगलवार को पूछे गए प्रश्न का उत्तर वह कैसे देंगी?
मेरा उत्तर
यदि इस प्रयोग को लाखों बार दोहराया जाए, तो हम तीन प्रकार की जागृतियाँ देखने की उम्मीद कर सकते हैं, जिनमें से प्रत्येक समान रूप से संभावित है:
- सिक्का सिर पर गिरता है, सोमवार को जागते हैं।
- सिक्का पूंछ पर गिरता है, सोमवार को जागता है।
- सिक्का पूंछ पर गिरता है, मंगलवार को जागता है।
ऐसा इसलिए है क्योंकि सोमवार को होने वाली जागृति, चित और पट के सिक्कों के बीच बराबर-बराबर बँटी होनी चाहिए। इसके अलावा, अगर सिक्का पट पर गिरता है, तो सोमवार और मंगलवार को होने वाली जागृति बिल्कुल बराबर होगी। इस प्रकार, एक बड़े नमूने के आकार में तीनों समूहों में लगभग समान संख्या में जागृति होगी।
इनमें से तीन में से एक जागरण चित आने पर होता है। इस प्रकार, सिक्के के चित पर आने की संभावना 1/3 है।
1/2 शिविर का तर्क है कि एसबी को प्रत्येक जागरण पर कोई अतिरिक्त जानकारी नहीं दी जाती है और इस प्रकार यह मान लेना चाहिए कि फ्लिप का प्रत्येक परिणाम समान रूप से संभावित था।
इसके लिए, मैं इस समस्या को 999,999 जागरणों तक बढ़ाऊँगा यदि सिक्का पट पर गिरे। चित आने के बाद दस लाख में से केवल एक जागरण होगा। इसलिए, किसी भी जागरण पर यह मान लेना बहुत आसान होगा कि यह पट आने के बाद होने वाले 999,999 जागरणों में से एक था। दूसरे शब्दों में, इस स्थिति में सही उत्तर 1,000,000 में से 1 होगा।
एक और विस्तार देते हुए, क्या होगा अगर एसबी को हर बार जागने पर सिक्के के उछाल की भविष्यवाणी करने के लिए कहा जाए। अगर वह सही अनुमान लगाती, तो वह $1,000 जीत जाती। अगर उसके पास "चित" कहने की रणनीति होती, तो वह (1/2)*$1,000 = $500 जीतने की उम्मीद कर सकती थी। अगर उसके पास "पूंछ" कहने की रणनीति होती, तो वह (1/2)*$2,000 = $1,000 जीतने की उम्मीद कर सकती थी। तो, सिर्फ़ यह तथ्य कि एसबी जागृत है, सिक्के के पट पर गिरने के पक्ष में है।
यदि मेरा स्पष्टीकरण स्पष्ट नहीं था तो विकिपीडिया पर स्लीपिंग ब्यूटी समस्या मुझसे कहीं अधिक गहराई से इस पर चर्चा करती है, जिसमें एसबी की अन्य संभावित प्रतिक्रियाएं भी शामिल हैं।
यह प्रश्न विज़ार्ड ऑफ़ वेगास में मेरे मंच पर पूछा गया और इस पर चर्चा की गई।


