जादूगर से पूछो #395
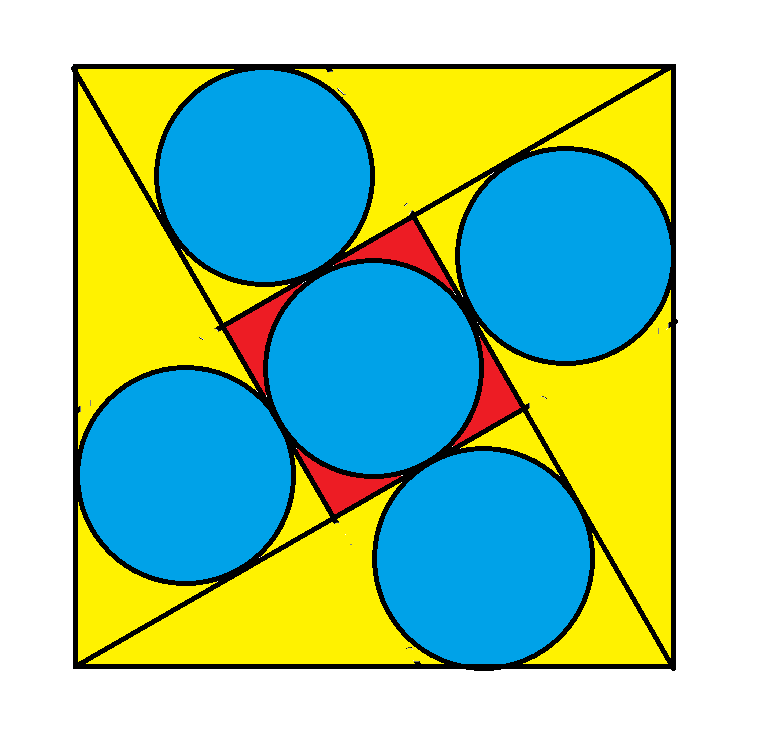
ऊपर दिए गए आरेख में चार समकोण त्रिभुज और एक बड़े वर्ग के अंदर एक छोटा वर्ग है। बड़े वर्ग की भुजा की लंबाई 1 है। सभी पाँच वृत्तों का व्यास समान है। त्रिज्या क्या है?
त्रिज्या = (sqrt(3)-1)/4 =~ 0.183013.
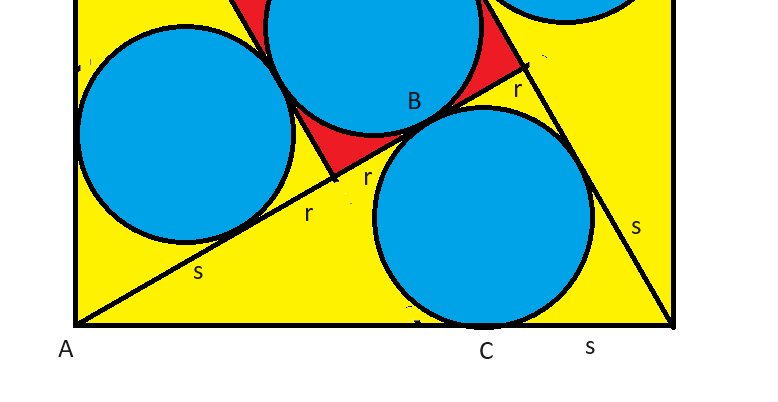 आइए इनमें से एक त्रिभुज पर विचार करें। आइए परिभाषित करें:
आइए इनमें से एक त्रिभुज पर विचार करें। आइए परिभाषित करें:- r = वृत्तों की त्रिज्या
- s = बड़े वर्ग के किसी भी कोने के बीच की दूरी और जहां निकटतम वृत्त उस त्रिभुज के स्पर्शरेखा है जिसमें वह अंकित है।
चित्र में त्रिभुज को देखने पर दूरियाँ इस प्रकार हैं:
- छोटा पैर = r+s
- लंबी भुजा = 3r+s
- कर्ण = 1
पाइथागोरस सूत्र का उपयोग:
(आर+एस) 2 + (3आर+एस) 2 = 1
आर 2 + 2आरएस + एस 2 + 9 आर 2 + 6आरएस + एस 2 = 1
10r 2 + 2s 2 + 8rs = 1
इसे हल करने के लिए हमें एक और समीकरण चाहिए। आइए बड़े वर्ग की लंबाई देखें, जो हमें 1 दी गई है। AB = AC। AB = 2r+s, इसलिए AC = 2r+s। बड़े वर्ग की शेष भुजा s है। इसलिए:
2आर + 2एस = 1.
2s = 1-2r
एस = 1/2 - आर
आइये इसे पाइटागोरस सूत्र से हमारे समीकरण में शामिल करें:
10r 2 + 2(1/2 - r) 2 + 8r(1/2 - r) = 1
10r 2 + 2(1/4 - r + r 2 ) + 4r - 8r 2 = 1
2आर 2 + 1/2 - 2आर + 2आर 2 + 4आर = 1
4r 2 + 2r - 1/2 = 0
8r 2 + 4r - 1 = 0
द्विघात समीकरण का उपयोग करते हुए:
आर = (-4 +/- sqrt(48))/16
आर = (वर्ग(3)-1)/4 =~ 0.183013।
यह समस्या माइंड योर डिसीजन्स यूट्यूब चैनल से ली गई है। प्रेश एक ऐसा समाधान प्रस्तुत करता है जिसके लिए पाइथागोरस सूत्र की आवश्यकता नहीं है।
[/spoiler]
यह समस्या मेरे फोरम विजार्ड ऑफ वेगास में पूछी गई और इस पर चर्चा की गई।
"सही और गलत रास्ता प्रणाली" के बारे में आपकी क्या राय है? यह इस तरह काम करती है कि खिलाड़ी एक यूनिट का "डोंट पास" दांव लगाता है। अगर कोई अंक आता है, तो खिलाड़ी उस नंबर पर एक यूनिट का दांव लगाता है। अगर वह अंक आता है, तो खिलाड़ी को मुनाफ़ा होता है और अगर वह सात से बाहर हो जाता है, तो वह बराबरी पर आ जाता है। यह एक फ्रीरोल जैसा लगता है। मैं क्या चूक रहा हूँ?
मान लीजिए कि अगर पॉइंट 4 या 10 है, तो खिलाड़ी केवल जीत पर ही 5% कमीशन देता है। हम वेगास के नियम का पालन करेंगे, जहाँ कम आउट रोल पर 12 का होना "डोंट पास बेट" पर पुश माना जाता है (उत्तरी नेवादा में वे 2 पर पुश करते हैं)। इसके बाद, यहाँ सभी संभावित परिणाम दिए गए हैं:
- 2 या 3 का रोल आने पर: खिलाड़ी पास न होने की शर्त पर एक यूनिट जीतता है।
- 12 का रोल आउट: खिलाड़ी पास न होने की शर्त पर आगे बढ़ता है।
- 7 या 11 का रोल आने पर: खिलाड़ी पास न होने की शर्त पर हार जाता है।
- 4 या 10 अंक और अंक जीत: खिलाड़ी खरीद दांव पर 1.95 यूनिट जीतता है और पास न करने पर एक यूनिट खो देता है, जिससे उसे 0.95 यूनिट की शुद्ध जीत मिलती है।
- 5 या 9 अंक और अंक जीत: खिलाड़ी प्लेस बेट पर 1.4 यूनिट जीतता है और पास न करने पर एक यूनिट हारता है, जिससे उसे 0.4 यूनिट की शुद्ध जीत मिलती है।
- 6 या 8 अंक और अंक जीत: खिलाड़ी प्लेस बेट पर 7/6 यूनिट जीतता है और पास न करने पर एक यूनिट हारता है, जिससे उसे 1/6 यूनिट की शुद्ध जीत मिलती है।
- 4 या 10 अंक होने पर अंक की हानि: खिलाड़ी खरीद दांव पर 1 इकाई खो देता है तथा नेट पुश के लिए पास न करने पर एक इकाई जीतता है।
- 5 या 9 का अंक और अंक की हानि: खिलाड़ी प्लेस बेट पर 1 यूनिट खो देता है और नेट पुश के लिए पास न करने पर एक यूनिट जीतता है।
- 6 या 8 का अंक और अंक की हानि: खिलाड़ी प्लेस बेट पर 1 यूनिट खो देता है और नेट पुश के लिए पास न करने पर एक यूनिट जीतता है।
निम्नलिखित तालिका सभी संभावित परिणामों का सारांश प्रस्तुत करती है। तालिका सभी संभावित परिणामों की संभावना, जीत और प्रतिफल में योगदान दर्शाती है। निचले दाएँ कक्ष में 0.02951 इकाइयों की अपेक्षित हानि दर्शाई गई है।
सही और गलत रास्ता प्रणाली
| आयोजन | भुगतान करता है | संभावना | वापस करना |
|---|---|---|---|
| 2 या 3 बाहर आओ | 1 | 0.083333 | 0.083333 |
| बाहर आओ 12 | 0 | 0.027778 | 0.000000 |
| 7 या 11 बजे बाहर आओ | -1 | 0.222222 | -0.222222 |
| प्वाइंट 4 की जीत | 0.95 | 0.027778 | 0.026389 |
| प्वाइंट 5 की जीत | 0.4 | 0.044444 | 0.017778 |
| अंक 6 की जीत | 0.166667 | 0.063131 | 0.010522 |
| प्वाइंट 8 की जीत | 0.166667 | 0.063131 | 0.010522 |
| प्वाइंट 9 की जीत | 0.4 | 0.044444 | 0.017778 |
| पॉइंट 10 की जीत | 0.95 | 0.027778 | 0.026389 |
| अंक 4 का नुकसान | 0 | 0.055556 | 0.000000 |
| अंक 5 का नुकसान | 0 | 0.066667 | 0.000000 |
| अंक 6 का नुकसान | 0 | 0.075758 | 0.000000 |
| अंक 8 का नुकसान | 0 | 0.075758 | 0.000000 |
| प्वाइंट 9 का नुकसान | 0 | 0.066667 | 0.000000 |
| 10 अंक का नुकसान | 0 | 0.055556 | 0.000000 |
| कुल | 1.000000 | -0.029512 |
इस रणनीति का अपेक्षित मूल्य नकारात्मक होने का कारण कम आउट रोल है। 2 या 3 पर जीतने के 3 तरीके हैं और 7 या 11 पर हारने के 8 तरीके हैं। यह सच है कि अगर खिलाड़ी कम आउट रोल पर बच जाता है तो उसके पास सकारात्मक इक्विटी होती है, लेकिन यह कम आउट रोल पर अपेक्षित नुकसान की भरपाई के लिए पर्याप्त नहीं है।
मेरी पत्नी 20% समय गुस्से में रहती है। जब उससे पूछा जाता है, "क्या आप गुस्से में हैं?" तो वह 90% बार गुस्से में "नहीं" कहती है। जब यही सवाल उससे बिना गुस्से के पूछा जाता है, तो वह 95% बार "नहीं" कहती है। मेरा सवाल है कि सवाल के जवाब के अनुसार उसके गुस्से में होने की क्या संभावना है?
यह एक क्लासिक बायेसियन प्रायिकता प्रश्न है।
यदि वह "नहीं" में उत्तर देती है, तो उसके पागल होने की संभावना 9/47 = 19.15% है।
यदि वह "हाँ" में उत्तर देती है, तो उसके पागल होने की संभावना 1/3 = 33.33% है।
"यदि A तो B" के रूप में व्यक्त प्रश्नों के उत्तर का सूत्र प्रायिकता (A और B दोनों)/प्रायिकता (B) है।
"नहीं" उत्तर के मामले में, उसके पागल होने की संभावना (0.2*0.9)/(0.2*0.9 + 0.8*0.95) = 0.18/0.94 = 9/47 है।
"हाँ" उत्तर के मामले में, उसके पागल होने की संभावना (0.2*0.1)/(0.2*0.1 + 0.8*0.05) = 0.02/0.06 = 1/3 है।
[/spoiler]

