WOO logo

विज़ार्ड अनुशंसा करता है

जादूगर से पूछो #383

ऐलिस और बिल को एक घर को पेंट करने में 3 घंटे लगते हैं।
ऐलिस और सिंडी को एक घर को पेंट करने में 4 घंटे लगते हैं।
बिल और सिंडी को एक घर को पेंट करने में 5 घंटे लगते हैं।

यदि वे सभी पेंटिंग करें तो कितना समय लगेगा?

गुमनाम

120/47 =~ 2.553191 घंटे

यहां मेरा समाधान (पीडीएफ) है।

एक रबर बैंड को 2 और 5 व्यास वाले दो आसन्न वृत्तों पर फैलाया गया है। फैले हुए रबर बैंड की लंबाई क्या है?

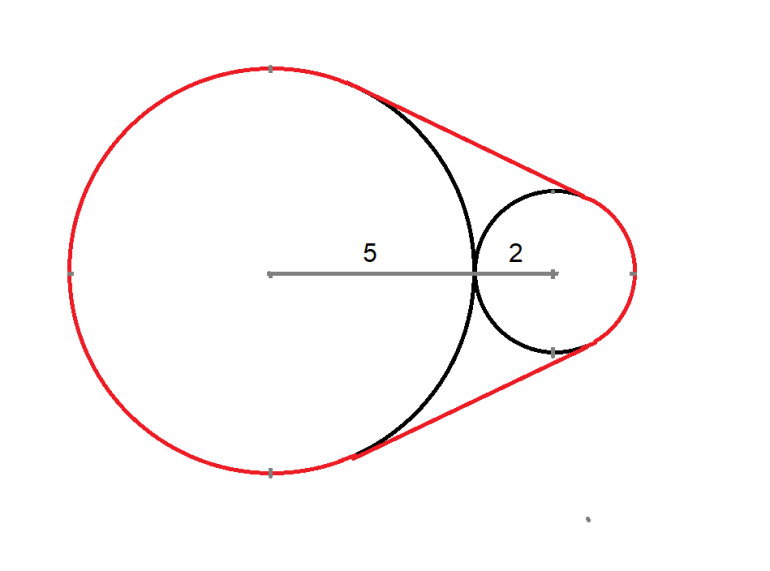
wizardofodds.com /wizfiles/img/3856/3565_large_two-circles-q.png">

गुमनाम

[स्पॉइलर=उत्तर] 2*sqrt(40) + 10*(π - cos -1 (3/7)) =~ 37.297725 [/स्पॉइलर]

यहां मेरा समाधान (पीडीएफ) है।

यह समस्या मेरे फोरम विजार्ड ऑफ वेगास में पूछी गई और चर्चा की गई।

पत्थर-कागज़-कैंची के एक खेल पर विचार करें जहाँ:

  • यदि पत्थर कैंची को हरा देता है, तो कैंची पत्थर को 1 डॉलर देगी
  • यदि कैंची कागज़ को हरा देती है, तो कागज़ कैंची को 2 डॉलर देगा
  • यदि कागज पत्थर को हरा देता है, तो पत्थर कागज को 3 डॉलर देगा
  • टाई पर पैसे का लेन-देन नहीं होता

मान लीजिए दो तर्कशास्त्री खेल रहे हैं। प्रत्येक के लिए सर्वोत्तम रणनीति क्या है?

गुमनाम

[स्पॉइलर=उत्तर]

  • 1/6 संभावना के साथ कागज खेलें
  • 1/3 संभावना के साथ रॉक खेलें
  • 1/2 संभावना के साथ कैंची खेलें
[/बिगाड़ने वाला]

[स्पॉइलर=समाधान]

आइए, अपनी जीत को अधिकतम करने की चाह रखने वाले तर्कशास्त्री के लिए कुछ संभावनाओं को परिभाषित करें:

  • r = रॉक बजाने की संभावना
  • p = कागज खेलने की संभावना
  • s = कैंची खेलने की प्रायिकता

यह स्पष्ट है कि r+p+s = 1. दिया गया है r और p, s = 1-rp.

यदि दो तर्कशास्त्री खेलते हैं, तो दोनों को अपने प्रतिद्वंद्वी के खेलने से कोई फर्क नहीं पड़ेगा, बशर्ते कि वे अपनी पसंद यादृच्छिक रूप से चुनें।

प्रतिद्वंद्वी प्ले रॉक की अपेक्षित जीत है: 3p-(1-rp) = 4p+r-1

प्रतिद्वंद्वी प्ले पेपर की अपेक्षित जीत है: 2(1-rp) - 3r = 2-5r-2p

प्रतिद्वंद्वी खेल कैंची की अपेक्षित जीत है: r - 2p

ये तीनों समीकरण बराबर होने चाहिए।

पहले और तीसरे को एक दूसरे के बराबर रखने पर हमें यह प्राप्त होता है:

4p+r-1 = r - 2p

पी = 1/6

प्रथम और द्वितीय को एक दूसरे के बराबर रखने पर हमें प्राप्त होता है:

2 -5r - 2p = 4p + r -1

हम पहले से ही जानते हैं कि p=1/6, जो हमें आसानी से r=1/3 तक ले जाता है।

एस=1-आरपी = 1-(1/3)-(1/6) = 1/2.

इसलिए, दोनों को 1/6 संभावना के साथ कागज, 1/3 संभावना के साथ पत्थर और 1/2 संभावना के साथ कैंची से खेलना चाहिए।

इस पहेली के लिए सामान्य मामला यह है कि प्रत्येक विकल्प को इस आधार पर खेला जाए कि यदि अन्य दो प्रतीकों को खेला जाता तो कितना धन हाथ बदलता।

[/बिगाड़ने वाला]

यह समस्या मेरे फोरम विजार्ड ऑफ वेगास में पूछी गई और चर्चा की गई।