जादूगर से पूछो #373
मुझे यकीन है कि आप बिग बैंग थ्योरी के प्रशंसक हैं। मेरे पसंदीदा दृश्यों में से एक रॉक पेपर सिज़र्स लिज़र्ड स्पॉक का खेल है। यह रॉक पेपर सिज़र्स के पाँच-चिन्हों वाले खेल जैसा है, जिसके नियम इस प्रकार हैं:
- कागज़ के कवर कमाल के हैं
- चट्टान ने छिपकली को कुचल दिया
- छिपकली ने स्पॉक को जहर दिया
- स्पॉक ने कैंची तोड़ दी
- कैंची कागज काटती है
- छिपकली कागज खाती है स्पॉक चट्टान को वाष्पीकृत करता है
- कैंची से छिपकली का सिर काटा
- पेपर ने स्पॉक को गलत साबित किया
- चट्टान ने कैंची को कुचल दिया
मेरा प्रश्न यह है कि क्या अधिक प्रतीकों को जोड़ा जा सकता है, जिससे प्रत्येक पक्ष को किसी यादृच्छिक खिलाड़ी के विरुद्ध समान अवसर प्राप्त हो सकें?
हाँ, मुझे भी वो सीन बहुत पसंद है! उसका यूट्यूब वीडियो यहाँ है।
आपको विषम संख्या में चिह्नों की आवश्यकता है। सिद्धांततः, आप सम संख्या भी रख सकते हैं, लेकिन फिर आपको ऐसे नियम बनाने होंगे जहाँ अलग-अलग चिह्नों के कुछ जोड़े बराबरी पर आएँ। नहीं, हम एक निर्णायक खेल चाहते हैं जहाँ केवल तभी बराबरी हो जब दोनों खिलाड़ी एक ही चिह्न खेलें।
अभाज्य संख्या के प्रतीकों के साथ एक हल विशेष रूप से सुंदर और समझाने में आसान होता है। उदाहरण के तौर पर, मुझे सात प्रतीकों के साथ समझाने की अनुमति दें। आइए, प्रतीकों A से G तक को लेबल करें और उन्हें नीचे दिए गए चित्र में एक वृत्त पर दर्शाएँ।
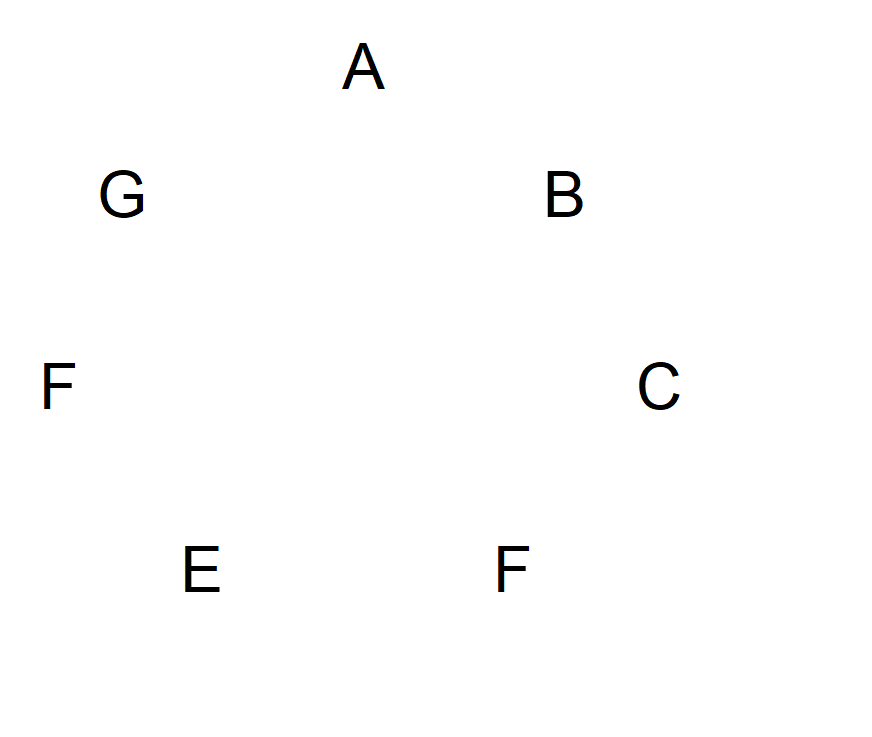
इसके बाद, A से शुरू करें और फिर दक्षिणावर्त दिशा में अगले चिह्न तक एक तीर बनाएँ। तीर इन दोनों के बीच वाले चिह्न की ओर इंगित करेगा। इसे ऐसे समझें जैसे उस चिह्न पर एक तीर से निशाना लगाया जा रहा हो। जब तक आप A पर वापस न आ जाएँ, तब तक दक्षिणावर्त दिशा में चलते रहें। चित्र ऐसा नहीं दिखेगा:
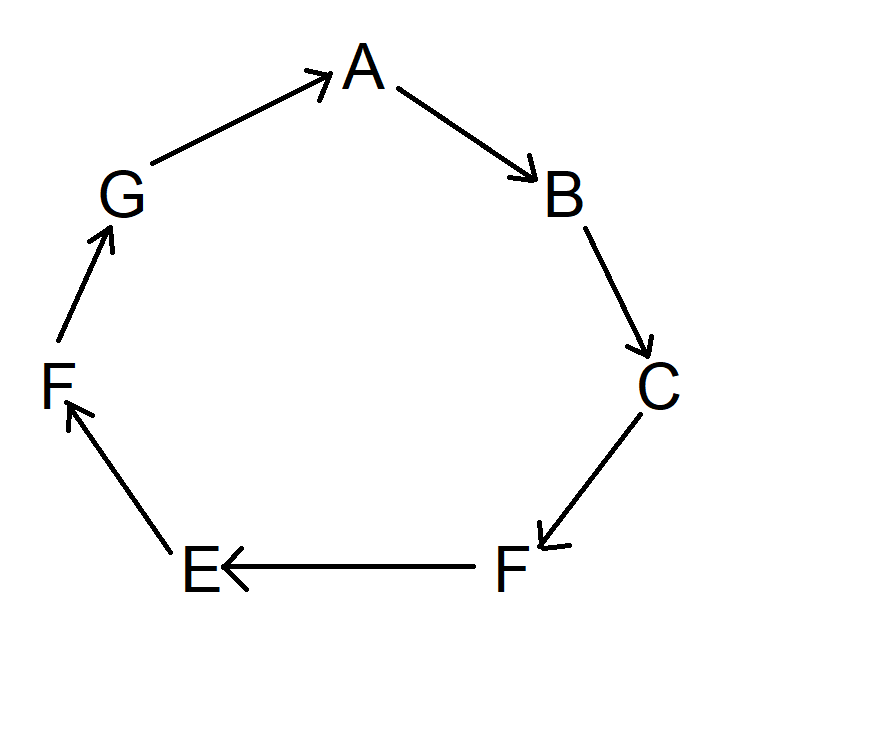
अब, यही प्रक्रिया दोहराएँ, लेकिन A से शुरू करते हुए, दो चिह्नों को दक्षिणावर्त घुमाएँ। दरअसल, आप अपनी इच्छानुसार कहीं से भी शुरू कर सकते हैं। अब आरेख इस तरह दिखता है:
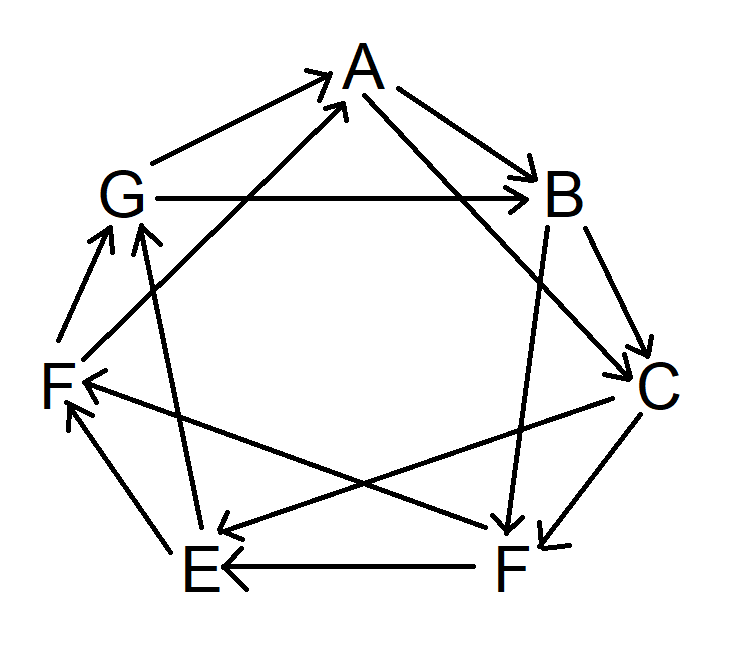
अंत में, यही प्रक्रिया दोहराएँ, लेकिन तीन चिह्नों को दक्षिणावर्त दिशा में छोड़ दें। अब आरेख इस प्रकार दिखाई देगा:
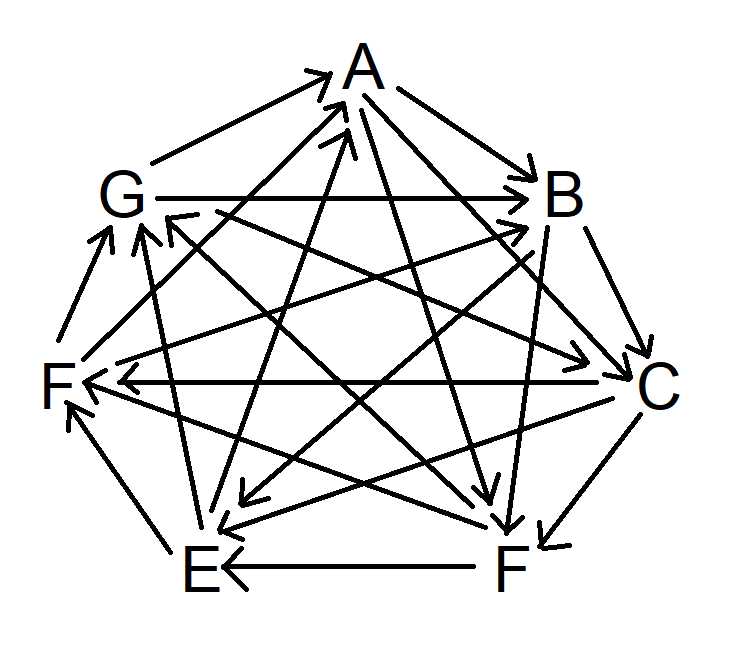
ध्यान दें कि इस बिंदु पर प्रत्येक प्रतीक तीन अन्य प्रतीकों को हराता है तथा तीन अन्य भिन्न प्रतीकों द्वारा पराजित होता है।
यह विधि किसी भी अभाज्य संख्या के प्रतीकों के लिए काम करेगी क्योंकि जब तक आप मूल प्रतीक पर वापस लौटेंगे, तब तक आप हर प्रतीक से गुज़र चुके होंगे। n प्रतीकों के लिए, आपको इस प्रक्रिया को (n-1)/2 बार दोहराना होगा।
आप किसी भी विषम संख्या में प्रतीकों के साथ एक संतुलित खेल बना सकते हैं, लेकिन कभी-कभी आप मूल प्रतीक पर बहुत जल्दी वापस लौट जाएँगे। ऐसा होने पर, आपको छूटे हुए प्रतीकों से शुरू करके दूसरे लूप बनाने होंगे।
यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।
थ्री कार्ड पोकर में टाई होने की संभावना क्या है?
सटीक उत्तर 450528/407170400 =~ 0.001106485 =~ 1/904 है।
निम्नलिखित तालिका प्रत्येक प्रकार के प्रारंभिक हाथ बनाने के तरीकों की संख्या और दूसरे हाथ में बराबरी पर आने वाले संयोजनों की संख्या दर्शाती है। स्ट्रेट्स और ट्रैश हाथों के मामले में, यह मायने रखता है कि पहले हाथ में दो या तीन सूट हैं।
नीचे दाएँ सेल में दिखाया गया है कि थ्री कार्ड पोकर में बराबरी करने के 450,528 तरीके हैं। दो हाथों के लिए संयोजनों की कुल संख्या combin(52,3)*combin(49,3) = 407170400 है। इस प्रकार, उत्तर 450528/407170400 है।
तीन कार्ड पोकर टाई
| हाथ | हाथ 1 | हाथ 2 | उत्पाद |
|---|---|---|---|
| तीन हास्य अभिनेता | 52 | 0 | 0 |
| स्ट्रेट फ्लश | 48 | 3 | 144 |
| सीधे (तीन सूट) | 288 | 26 | 7,488 |
| सीधे (दो सूट) | 432 | 25 | 10,800 |
| लालिमा | 1,096 | 3 | 3,288 |
| जोड़ा | 3,744 | 3 | 11,232 |
| जंक (तीन सूट) | 6,576 | 26 | 170,976 |
| जंक (दो सूट) | 9,864 | 25 | 246,600 |
| कुल | 22,100 | 450,528 |
6-5 ब्लैकजैक में मुफ्त ऐस कूपन का मूल्य क्या है?
मेरे निःशुल्क ऐस पृष्ठ के मूल्य में मैं बताता हूं कि इसका मूल्य 3-2 ब्लैकजैक में शर्त राशि का 50.1844% है।
छह-डेक वाले ब्लैकजैक में, पहला पत्ता इक्का होने पर, जीतने वाले ब्लैकजैक की संभावना 29.3139% होती है। ऐसा होने पर, आप 6-5 ब्लैकजैक में 3-2 की तुलना में 0.3 यूनिट कम जीतते हैं।
तो 6-5 सिक्स-डेक ब्लैकजैक में एक फ्री ऐस का मूल्य प्रारंभिक दांव का 50.1844% × 29.3139 × 0.3 = 41.3902% है।
किसी ने मुझे शर्त लगाने की चुनौती दी थी कि वह 27 पासों में दो पासों से कुल 12 पासे फेंक सकता है। अगर वह ऐसा नहीं करता, तो मैं बराबर पैसे जीत जाता। चूँकि 12 आने की संभावना 1/36 है, तो क्या उसे 12 आने में औसतन 36 पासे नहीं लगाने चाहिए? ऐसा लगता है कि अगर मेरे प्रतिद्वंद्वी को सिर्फ़ 27 पासे ही फेंके जाते, तो संभावनाएँ मेरे पक्ष में होतीं। क्या मैं सही हूँ या मेरे गणित में कोई खामी है?
12 के बीच औसत प्रतीक्षा समय वास्तव में 36 रोल के बराबर है, जिसमें 12 का रोल भी शामिल है। हालाँकि, इसका मतलब यह नहीं है कि वे हर 36 रोल पर आते हैं। 12 न आने की संभावना (35/36) है। 27 रोल में ऐसा न होने की संभावना (35/36)^27 है। इसलिए, कम से कम 12 आने की संभावना 1-(35/36)^27 = 53.26% है।
नीचे दी गई तालिका 20 से 36 रोल के लिए कम से कम 12 रोल की संभावना दर्शाती है। ध्यान दें कि सम-धन पर लाभ के लिए 25 रोल की आवश्यकता होती है।
संभावना 12
| रोल्स | संभावना |
|---|---|
| 20 | 43.07% |
| 21 | 44.66% |
| 22 | 46.19% |
| 23 | 47.69% |
| 24 | 49.14% |
| 25 | 50.55% |
| 26 | 51.93% |
| 27 | 53.26% |
| 28 | 54.56% |
| 29 | 55.82% |
| 30 | 57.05% |
| 31 | 58.24% |
| 32 | 59.40% |
| 33 | 60.53% |
| 34 | 61.63% |
| 35 | 62.69% |
| 36 | 63.73% |


