जादूगर से पूछो #367
मुझे क्रेप्स में सभी नंबरों पर दांव लगाना पसंद है। 7-आउट से पहले मैं कितने अनोखे नंबरों पर दांव लगाने की उम्मीद कर सकता हूँ?
अन्य पाठकों के लाभ के लिए, प्रश्न यह है कि निम्नलिखित में से कितने योगों को सात आने से पहले दो पासों से उछाला जाएगा: 4, 5, 6, 8, 9, और 10।
उत्तर 2.375758 है। निम्न तालिका निर्दिष्ट सीमा में शून्य से छह अद्वितीय योग आने की प्रत्येक व्यक्तिगत संभावना की प्रायिकता दर्शाती है। निचला दायाँ कक्ष सात आने से पहले आने वाले औसत अद्वितीय योगों को दर्शाता है।
अद्वितीय संख्याएँ निकाली गईं
| कुल | संभावना | अपेक्षित |
|---|---|---|
| 6 | 0.062168 | 0.373009 |
| 5 | 0.101016 | 0.505079 |
| 4 | 0.129245 | 0.516979 |
| 3 | 0.151531 | 0.454594 |
| 2 | 0.170057 | 0.340114 |
| 1 | 0.185983 | 0.185983 |
| 0 | 0.200000 | 0.000000 |
| कुल | 1.000000 | 2.375758 |
क्या यह सच है कि एक निष्पक्ष सिक्के के उछाले जाने पर, उस तरफ गिरने की अधिक संभावना होती है, जिस तरफ से वह उछलकर शुरू हुआ था?
सबूत बताते हैं कि यह सच है!
स्टैनफोर्ड विश्वविद्यालय के पर्सी डायकोनिस और सुसान होम्स ने 10,000 सिक्कों की उछाल दर्ज की। 50.8% बार सिक्का उसी तरफ़ गिरा जिस तरफ़ से वह शुरू हुआ था (स्रोत: अमेरिकन मैथमेटिकल सोसाइटी के न्यूज़लेटर "व्हाट्स हैपनिंग इन द मैथमेटिकल साइंसेज" से लिया गया इक्यावन परसेंट सॉल्यूशन )। इतने ज़्यादा या उससे ज़्यादा अनुपात की संभावना 5.48% है।
इसे गणितीय रूप से सिद्ध करने के लिए, मैंने मान लिया कि एक सिक्के के वास्तविक चक्करों की संख्या पॉइसन वितरण का पालन करती है। अधिक विशिष्ट रूप से, यदि चक्करों की माध्य संख्या m थी, तो ठीक n चक्करों की प्रायिकता exp(-m)*m^n/n! है। पॉइसन वितरण को स्पष्ट करने के लिए, निम्नलिखित ग्राफ़ 0 से 25 चक्करों की प्रायिकता दर्शाता है, जिसका माध्य 10 है।
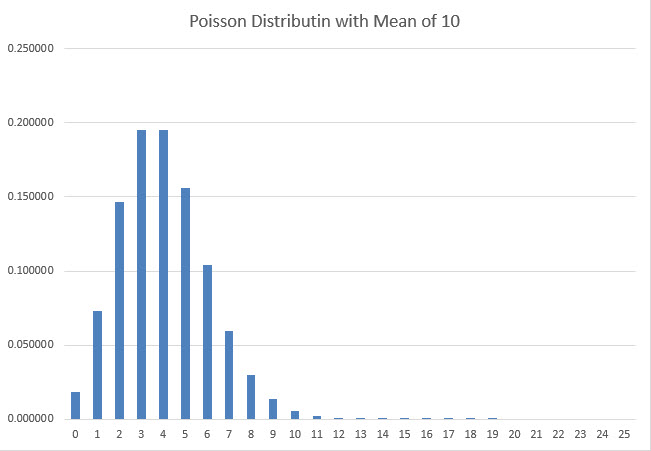
मैंने पॉइसन धारणा को इसलिए चुना क्योंकि यह पर्याप्त रूप से बड़े माध्य के लिए लगभग घंटी वक्र आकार का अनुसरण करती है और वास्तविक परिणाम कभी भी शून्य से नीचे नहीं जा सकता।
फिर मैंने अर्ध-चक्रों के विभिन्न माध्यों के लिए अर्ध-चक्रों की सम संख्या (जिसके परिणामस्वरूप प्रारंभिक स्थिति के समान ही भुजा ऊपर की ओर उतरती है) की प्रायिकता की गणना की। निम्न तालिका 0.5 से 5.0 माध्यों के परिणाम दर्शाती है।
सम और विषम संख्या में चक्करों की संभावना
| औसत क्रांतियाँ | सम कुल | विषम कुल |
|---|---|---|
| 0.5 | 0.567667642 | 0.432332358 |
| 1 | 0.509157819 | 0.490842181 |
| 1.5 | 0.501239376 | 0.498760624 |
| 2 | 0.500167731 | 0.499832269 |
| 2.5 | 0.500022700 | 0.499977300 |
| 3 | 0.500003072 | 0.499996928 |
| 3.5 | 0.500000416 | 0.499999584 |
| 4 | 0.500000056 | 0.499999944 |
| 4.5 | 0.500000008 | 0.499999992 |
| 5 | 0.500000001 | 0.499999999 |
फिर मैं सोचने लगा कि सम संख्या की प्रायिकता हमेशा 50% से ज़्यादा क्यों होती है। पता चला कि सम संख्या की प्रायिकता, जिसका माध्य m दिया गया हो, 0.5 + e^(-2m)/2 के रूप में व्यक्त की जा सकती है। e की घात किसी भी चीज़ की धनात्मक होनी चाहिए, इसलिए सम संख्या में चक्करों की प्रायिकता भी धनात्मक होती है।
आप इस सूत्र का मेरा प्रमाण यहां देख सकते हैं।
प्राइस इज राइट पर स्पेलिंग बी गेम के बारे में आपका विश्लेषण क्या है?
अन्य पाठकों के लाभ के लिए, मैं पहले नियमों पर चर्चा कर लूँगा।
- एक बोर्ड पर 30 कार्ड हैं, जिन पर 1 से 30 तक की संख्या अंकित है।
- प्रत्येक कार्ड के पीछे एक अक्षर या शब्द "कार" लिखा होता है। प्रत्येक कार्ड का वितरण इस प्रकार है:
- सी: 11
- उत्तर: 11
- आर: 6
- कार: 2
- मेजबान खिलाड़ी को दो कार्ड चुनने देता है।
- मूल्य निर्धारण खेल के बाद, जिसके बारे में मैं नहीं बताऊंगा, खिलाड़ी को तीन और कार्ड अर्जित करने का अवसर मिलता है।
- कार्ड उलट दिए जाएंगे।
- खिलाड़ी दो तरीकों से कार जीत सकता है:
- खिलाड़ी को प्रत्येक अक्षर का कम से कम एक कार्ड मिलता है (इस प्रकार CAR शब्द की वर्तनी बनती है)।
- खिलाड़ी को कम से कम एक "CAR" कार्ड मिलता है।
- खेल के किसी भी समय, खिलाड़ी आत्मसमर्पण कर सकता है और अपने बचे हुए प्रत्येक कार्ड के लिए 1,000 डॉलर प्राप्त कर सकता है।
यहां खेले जा रहे खेल की एक क्लिप है।
निम्नलिखित तालिका में जीतने की संभावना को दर्शाया गया है, जो इस बात पर निर्भर करता है कि खिलाड़ी के पास कितने कार्ड हैं, यह मानते हुए कि अभी तक कोई भी कार्ड नहीं दिया गया है।
स्पेलिंग बी - जीतने की संभावना
| कार्ड | संभावना जीत |
|---|---|
| 2 | 0.131034 |
| 3 | 0.371921 |
| 4 | 0.584018 |
| 5 | 0.734888 |
किसी भी कार्ड को पलटने से पहले, खिलाड़ी को कार का कोई भी उचित मूल्य मानकर उसे सरेंडर नहीं करना चाहिए। उदाहरण के लिए, केवल दो कार्ड होने पर भी, खिलाड़ी के पास कम से कम एक CAR कार्ड होने की 13.1% संभावना होती है। अगर कार का मूल्य $15,263.16 है, तो खिलाड़ी को $2,000 के सरेंडर मूल्य से कोई फर्क नहीं पड़ना चाहिए। किसी भी नई कार की कीमत इससे ज़्यादा होगी।
खिलाड़ी के पास कितने कार्ड बचे हैं, उसके अनुसार कार के मूल्य पर निम्नलिखित उदासीनता अंक हैं।
स्पेलिंग बी - जीतने की संभावना
| कार्ड | उदासीनता बिंदु |
|---|---|
| 2 | $15,263.16 |
| 3 | $8,066.23 |
| 4 | $6,849.11 |
| 5 | $6,803.75 |


