जादूगर से पूछो #355
फिल्म लाइसेंस टू किल में, जेम्स बॉन्ड ब्लैकजैक के तीन राउंड खेलता है, एक बार में पाँच हाथ खेलता है। मैंने देखा है कि वह एक बार भी किसी में सफल नहीं होता। इसकी संभावना कितनी है?
आपको इस दृश्य की क्लिप यूट्यूब पर मिल सकती है।
खेल में बड़े पत्तों की संख्या संदिग्ध रूप से ज़्यादा दिखाई देती है, है ना? ये वो पत्ते हैं जो मैं पहचान पाया। ध्यान दें कि कुछ मामलों में, पत्ते साफ़ दिखाई नहीं दे रहे थे।
हत्या का लाइसेंस - रैंक का अवलोकन
| रैंक | देखा |
|---|---|
| 2 | 0 |
| 3 | 0 |
| 4 | 0 |
| 5 | 2 |
| 6 | 2 |
| 7 | 1 |
| 8 | 4 |
| 9 | 4 |
| 10 | 8 |
| जे | 3 |
| क्यू | 6 |
| कश्मीर | 4 |
| ए | 1 |
| कुल | 35 |
आप बिलकुल सही कह रहे हैं, बॉन्ड अपने शुरुआती 15 हाथों में से किसी पर भी हिट नहीं करता। वह एक बार आठों को विभाजित करता है, लेकिन विभाजित करने के बाद भी हिट नहीं करता। यहाँ सभी 15 हाथों पर उसके शुरुआती एक्शन की गिनती दी गई है:
- डबल — 1
- विभाजित — 1
- स्टैंड — 13
यहां प्रत्येक प्रारंभिक कार्रवाई की बुनियादी रणनीति संभावनाएं दी गई हैं, जिसमें छह डेक, विभाजन के बाद डबल की अनुमति, डीलर द्वारा होल कार्ड पर नजर डालना और डीलर द्वारा सॉफ्ट 17 पर खड़ा होना शामिल है।
ब्लैकजैक -- पहली कार्रवाई की संभावनाएं
| कार्रवाई | संभावना |
|---|---|
| खड़ा होना | 43.46% |
| मार | 39.78% |
| दोहरा | 9.53% |
| विभाजित करना | 2.48% |
| डांडा | 4.75% |
| कुल | 100.00% |
यदि आत्मसमर्पण की अनुमति दी जाती, तो यह संभावना 4.14% होती, जो खड़े रहने की संभावना से बाहर होती।
यह ध्यान देने योग्य है कि बॉन्ड एक बार 16 बनाम 10 पर खड़ा था। बुनियादी रणनीति यही है कि उसे हिट किया जाए, लेकिन यह बहुत मामूली है। उस हाथ से निकले दहाई के ढेर को देखते हुए, बॉन्ड को शायद पता था कि गिनती ज़्यादा है, जिससे उस स्थिति में खड़े होने पर एक बुनियादी रणनीति अपवाद लागू हो जाता।
किसी एक हाथ के न लगने की संभावना 60.22% है। यह मानते हुए कि प्रत्येक हाथ स्वतंत्र है, 15 में से 15 के न लगने की संभावना 2015 में 0.602162 15 = 0.000496253 = लगभग 1 है।
स्क्विड गेम में, 16 खिलाड़ी एक काँच के पुल के साथ खेलते हैं। यह पुल काँच के 18 जोड़ों में बँटा होता है। हर जोड़े में, काँच का एक टुकड़ा टेम्पर्ड होता है और एक खिलाड़ी का वज़न सहन कर सकता है। जोड़े का दूसरा टुकड़ा साधारण काँच का होता है और खिलाड़ी के वज़न से टूट जाएगा। अगर कोई खिलाड़ी साधारण काँच के टुकड़े पर पैर रखता है, तो वह टूट जाएगा और गिरकर उसकी मौत हो जाएगी।
खिलाड़ियों को पूर्वनिर्धारित क्रम में एक-एक करके आगे बढ़ना होगा।
कांच की सीढ़ियों के प्रत्येक जोड़े पर यादृच्छिक अनुमान लगाते हुए, सुरक्षित रूप से पार करने वाले खिलाड़ियों की अपेक्षित संख्या क्या है?
मैं उत्तर और समाधान को स्पॉयलर टैग में डाल दूंगा, ताकि दुनिया को स्वयं उत्तर ढूंढने में आनंद आए।
[स्पॉइलर=समाधान]
खिलाड़ी 1 के सुरक्षित रूप से पार करने की संभावना (1/2)^18 = 1/262144 = लगभग 0.000004 है।
खिलाड़ी 2 के सुरक्षित रूप से पार करने के दो तरीके हैं:
- खिलाड़ी 1 सुरक्षित रूप से पार कर जाता है। इस स्थिति में, खिलाड़ी 2 उसके कदमों की नकल कर सकता है।
- खिलाड़ी 1 और खिलाड़ी 2 के बीच केवल एक ही गलत कदम है। यह काँच के संभावित जोड़ों में से 18 पर हो सकता है। 17 अच्छे कदमों और एक गलत कदम की प्रायिकता 18*(1/2)^2 = 18/262144 = 0.000069 है।
इसलिए, खिलाड़ी 2 के सुरक्षित रूप से पार करने की संभावना 0.000004 + 0.000069 = 0.000072 है।
खिलाड़ी 3 के सुरक्षित रूप से पार करने के दो तरीके हैं:
- खिलाड़ी 2 सुरक्षित रूप से पार कर जाता है। इस स्थिति में, खिलाड़ी 3 उसके कदमों की नकल कर सकता है।
- खिलाड़ी 1, 2 और 3 के बीच केवल दो ही गलत कदम हैं। खिलाड़ी 1 और 2 को मारने वाले दो मोहरों के लिए काँच के 18 जोड़ों में से 2 को चुनने के लिए संयुक्त(18,2)=153 तरीके हैं। 16 अच्छे कदमों और दो गलत कदमों की प्रायिकता 153*(1/2)^2 = 153/262144 = 0.000584 है।
इसलिए, खिलाड़ी 3 के सुरक्षित रूप से पार करने की संभावना 0.000072 + 0.000584 = 0.000656 है।
खिलाड़ी 4 के सुरक्षित रूप से पार करने के दो तरीके हैं:
- खिलाड़ी 3 सुरक्षित रूप से क्रॉस कर लेता है। ऐसे में, खिलाड़ी 4 उसके कदमों की नकल कर सकता है।
- खिलाड़ी 1 से 4 के बीच, केवल तीन ही गलत कदम हैं। खिलाड़ी 1 से 3 को मारने वाले दो मोहरों के लिए काँच के 18 जोड़ों में से 3 को चुनने के लिए संयुक्त (18,3) = 816 तरीके हैं। 15 अच्छे कदमों और 3 गलत कदमों की प्रायिकता 816*(1/2)^2 = 816/262144 = 0.003113 है।
इस तर्क के आधार पर, हमें प्रत्येक खिलाड़ी की संभावना की निम्नलिखित तालिका प्राप्त होती है।
ब्रिज गेम
| खिलाड़ी | संभावना उत्तरजीविता |
|---|---|
| 1 | 0.000004 |
| 2 | 0.000072 |
| 3 | 0.000656 |
| 4 | 0.003769 |
| 5 | 0.015442 |
| 6 | 0.048126 |
| 7 | 0.118942 |
| 8 | 0.240341 |
| 9 | 0.407265 |
| 10 | 0.592735 |
| 11 | 0.759659 |
| 12 | 0.881058 |
| 13 | 0.951874 |
| 14 | 0.984558 |
| 15 | 0.996231 |
| 16 | 0.999344 |
| कुल | 7.000076 |
उत्तर को बंद रूप में व्यक्त करने के लिए, यह है:
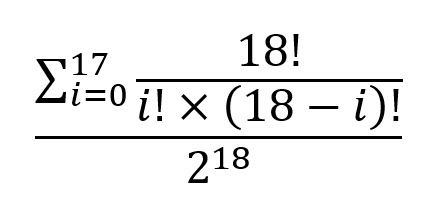
यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।
आपके अल्टीमेट एक्स गोल्ड में, 3:10 पर आपको एक पैट फुल हाउस, तीन ओवर फोर, दिया जाता है। 2 से 4 तक के किसी भी तरह के चार के लिए आपका गुणक 9x था। फुल हाउस के लिए गुणक 1x था। आपने सिर्फ़ तीन 3 के बजाय पैट फुल हाउस क्यों रखा और बड़े गुणक वाले चार के लिए प्रयास क्यों किया?
आप सही कह रहे हैं, मैंने उस हाथ से इसे पूरी तरह से बर्बाद कर दिया।
याद कीजिए, मैं 10-प्ले खेल रहा था। इस प्रकार, फुल हाउस होने पर मेरी जीत 10×35 = 350 थी।
केवल तीन हाथ होने पर, प्रत्येक हाथ की निम्नलिखित सम्भावनाएं थीं:
- एक ही तरह के चार - 4.26%
- फुल हाउस — 6.11%
- एक तरह के तीन - 89.64%
गुणकों के बाद प्रत्येक हाथ के लिए जीत इस प्रकार है:
- एक ही तरह के चार - 1800
- फुल हाउस — 35
- एक तरह के तीन - 15
सिर्फ़ तीन हाथ रखने पर मेरा अपेक्षित रिटर्न (4.26% * 1800) + (6.11% * 35) + (89.64% * 15) = 92.17854 होता। यह फुल हाउस के लिए 35 से काफ़ी ज़्यादा है। तो हाँ, मैंने उस हाथ में एक शर्मनाक गलती की।
किसी ने मुझे निम्नलिखित शर्त लगाने की चुनौती दी। मुझे एक मानक पोकर डेक से कोई भी तीन रैंक चुननी होती हैं, अपनी भविष्यवाणी लिखनी होती है, लेकिन उसे अंत तक छिपाए रखना होता है। उदाहरण के लिए, 7-इक्का-2। फिर उसने मुझसे बराबर की शर्त लगाने की पेशकश की कि अगर वह तीन अनुमान लगाता है तो वह मेरी कम से कम एक रैंक बता सकता है। मेरे जीतने की संभावना क्या थी?
जीतने के लिए, आपके प्रतिद्वंद्वी को तीनों भविष्यवाणियों में गलत होना होगा। पहली भविष्यवाणी के गलत होने की संभावना 10/13 है। दूसरी भविष्यवाणी के गलत होने की संभावना 9/12 है, क्योंकि हम संभावना के रूप में अनुमानित पहली रैंक को हटा सकते हैं। तीसरी भविष्यवाणी के गलत होने की संभावना 8/11 है, क्योंकि हम संभावना के रूप में अनुमानित पहली दो रैंक को हटा सकते हैं।
जीतने के लिए ये तीनों चीज़ें होनी ज़रूरी हैं। इस प्रकार, आपके जीतने की संभावना (10/13) * (9/12) * (8/11) = 720/1716 = 41.96% है।
सम राशि पर, इस दांव पर आपकी ओर से हाउस एज 16.08% है (ओह!)।
यह प्रश्न ओवेन ई'शे (संख्या 7) द्वारा लिखित द बुक ऑफ प्रोपोज़िशन बेट्स से लिया गया था।


