जादूगर से पूछो #353
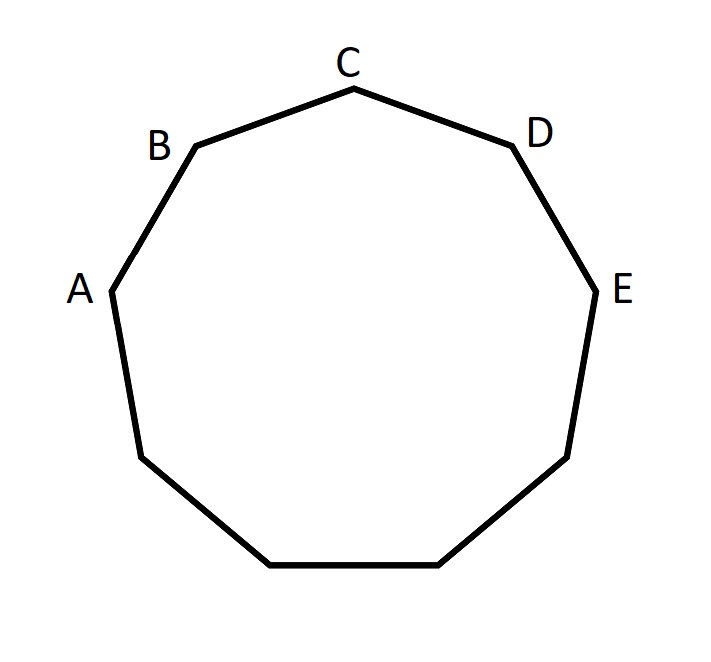
उपरोक्त आकृति एक भुजा की लम्बाई वाली एक नौभुज है।
कौन अधिक है, AB+AC या AE?
यह समस्या मेन्सा बुलेटिन के मार्च 2021 अंक से ली गई है।
इस समस्या का मेरा समाधान यहां है। (पीडीएफ)
मैं किसी भी तीन या चार अंकों वाली संख्या का वर्गमूल आसानी से कैसे ज्ञात कर सकता हूँ, यह मानते हुए कि उत्तर एक पूर्णांक है?
निम्नलिखित तालिका में 0 से 9 तक की संख्याएं, प्रत्येक का वर्ग तथा उस वर्ग का अंतिम अंक दर्शाया गया है।
वर्ग संख्याओं का अंतिम अंक
| मूल संख्या | वर्ग | अंतिम अंक वर्ग का |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 4 | 4 |
| 3 | 9 | 9 |
| 4 | 16 | 6 |
| 5 | 25 | 5 |
| 6 | 36 | 6 |
| 7 | 49 | 9 |
| 8 | 64 | 4 |
| 9 | 81 | 1 |
ध्यान दें कि सम वर्ग वाली संख्याएँ हमेशा 0, 1, 4, 5, 6, या 9 पर समाप्त होती हैं। यह सभी वर्गों के लिए सत्य है। ऐसा इसलिए है क्योंकि मूल संख्या का अंतिम अंक वर्ग के अंतिम अंक को निर्धारित करता है।
चरण 1: वर्ग के अंतिम अंक के आधार पर, हम वर्गमूल के अंतिम अंक को कम करने के लिए निम्न तालिका का उपयोग कर सकते हैं। उदाहरण के लिए, यदि 2809 वर्ग है, तो वर्गमूल का अंतिम अंक 3 या 7 होगा।
मूल संख्या का अंतिम अंक
| अंतिम अंक वर्गमूल का | अंतिम अंक वर्ग का |
|---|---|
| 0 | 0 |
| 1 | 1 या 9 |
| 4 | 2 या 8 |
| 5 | 5 |
| 6 | 4 या 6 |
| 9 | 3 या 7 |
चरण 2: अब, मूल संख्या लें और उसके दाएँ दो अंक हटा दें। उदाहरण के लिए, यदि मूल संख्या 2809 थी, तो 28 का प्रयोग करें।
चरण 3: चरण 2 के परिणाम से छोटी या बराबर सबसे छोटी वर्ग संख्या ज्ञात कीजिए। फिर, उस वर्ग संख्या का वर्गमूल निकालें। उदाहरण के लिए, 28 से छोटा सबसे छोटा वर्ग 25 है। 25 का वर्गमूल निकालें और आपको 5 प्राप्त होगा।
यदि आपने 100 तक के वर्ग याद नहीं किए हैं, तो आप निम्न तालिका का उपयोग कर सकते हैं।
वर्गमूल का पहला भाग
| चरण दो | चरण 3 |
|---|---|
| 1 से 3 | 1 |
| 4 से 8 | 2 |
| 9 से 15 | 3 |
| 16 से 24 | 4 |
| 25 से 35 | 5 |
| 36 से 48 | 6 |
| 49 से 63 | 7 |
| 64 से 80 | 8 |
| 81 से 99 | 9 |
चरण 4: यदि चरण 1 का परिणाम 0 या 5 है, तो उसे चरण 3 के परिणाम के बाद रखें और आपका काम पूरा हो गया।
अन्यथा, मान लीजिए कि चरण 3 का परिणाम a = है। मान लीजिए b=a×(a+1)। उदाहरण के लिए, यदि चरण 3 का परिणाम 5 है, तो b=5×6=30 है।
चरण 5: यदि b < a, तो वर्गमूल का अंतिम अंक चरण 1 की संभावनाओं में से छोटा होगा। अन्यथा, यदि b >= a, तो यह दो संभावनाओं में से बड़ा होगा।
चरण 6: वर्गमूल निकालने के लिए, चरण 3 से परिणाम लें और फिर चरण 5 से परिणाम प्राप्त करें। दूसरे शब्दों में 10×(चरण 3)+चरण 5।
आइये कुछ उदाहरण देखें:
256 का वर्गमूल ज्ञात करें।
- चरण 1: वर्गमूल का अंतिम अंक 4 या 6 है।
- चरण 2: अंतिम दो अंक हटाने पर हमें 2 प्राप्त होता है।
- चरण 3: 2 से छोटा या उसके बराबर सबसे छोटा वर्ग 1 है। 1 का वर्गमूल 1 है।
- चरण 4: 1*(1+1) = 2.
- चरण 5: चरण 4 का परिणाम चरण 2 के परिणाम के बराबर है, इसलिए हम चरण 1 के विकल्पों में से बड़े अंक को अंतिम अंक के रूप में उपयोग करते हैं, जो कि 6 है।
- चरण 6: वर्गमूल, 3 के परिणाम को चरण 5 के परिणाम से जोड़कर प्राप्त किया जाता है, जो 1 & 6 = 16 आता है।
1369 का वर्गमूल ज्ञात करें।
- चरण 1: वर्गमूल का अंतिम अंक 3 या 7 है।
- चरण 2: अंतिम दो अंक हटाने पर हमें 13 प्राप्त होता है।
- चरण 3: 13 से छोटा या उसके बराबर सबसे छोटा वर्ग 9 है। 9 का वर्गमूल 3 है।
- चरण 4: 3*(1+3) = 12.
- चरण 5: चरण 2 का परिणाम चरण 4 के परिणाम से बड़ा है, इसलिए हम चरण 1 के विकल्पों में से बड़े अंक को अंतिम अंक के रूप में उपयोग करते हैं, जो कि 7 है।
- चरण 6: वर्गमूल, 3 के परिणाम को चरण 5 के परिणाम से जोड़कर प्राप्त किया जाता है, जो 3 & 7 = 37 आता है।
2704 का वर्गमूल ज्ञात कीजिए।
- चरण 1: वर्गमूल का अंतिम अंक 2 या 8 है।
- चरण 2: अंतिम दो अंक हटाने पर हमें 27 प्राप्त होता है।
- चरण 3: 27 से कम या उसके बराबर सबसे छोटा वर्ग 25 है। 25 का वर्गमूल 5 है।
- चरण 4: 5*(1+5) = 60.
- चरण 5: चरण 2 का परिणाम चरण 4 के परिणाम से छोटा है, इसलिए हम चरण 1 के विकल्पों में से छोटे अंक को अंतिम अंक के रूप में उपयोग करते हैं, जो कि 2 है।
- चरण 6: वर्गमूल, 3 के परिणाम को चरण 5 के परिणाम से जोड़कर प्राप्त किया गया परिणाम है, जो 5 & 2 = 52 आता है।
5625 का वर्गमूल ज्ञात कीजिए।
- चरण 1: वर्गमूल का अंतिम अंक 5 है।
- चरण 2: अंतिम दो अंक हटाने पर हमें 56 प्राप्त होता है।
- चरण 3: 56 से छोटा या उसके बराबर सबसे छोटा वर्ग 49 है। 49 का वर्गमूल 7 है।
- चरण 4: चरण 1 का परिणाम 0 या 5 है, इसलिए उत्तर चरण 3 का परिणाम है जिसमें चरण 1 का परिणाम जोड़ा गया है: 7 और 5 = 75
6561 का वर्गमूल ज्ञात कीजिए।
- चरण 1: अंतिम अंक 1 या 9 है।
- चरण 2: अंतिम दो अंक हटाने पर हमें 65 प्राप्त होता है।
- चरण 3: 65 से कम या उसके बराबर सबसे छोटा वर्ग 64 है। 64 का वर्गमूल 8 है।
- चरण 4: 8*(1+8) = 72.
- चरण 5: चरण 2 का परिणाम चरण 4 के परिणाम से कम है, इसलिए हम चरण 1 के विकल्पों में से कम वाले विकल्प को अंतिम अंक के रूप में उपयोग करते हैं, जो कि 1 है।
- चरण 6: वर्गमूल, 3 के परिणाम को चरण 5 के परिणाम से जोड़कर प्राप्त किया गया परिणाम है, जो 8 और 1 = 81 आता है।
आप इस विधि का प्रदर्शन यूट्यूब पर देख सकते हैं।
ब्लैकजैक खेलने के 12 घंटों में, लगातार 60 या अधिक जीत देखने की संभावना क्या है?
उदार स्ट्रिप नियमों के आधार पर, ब्लैकजैक पृष्ठ में मेरे भिन्नता के अनुसार, शुद्ध जीत, धक्का या हार की संभावनाएं निम्नलिखित हैं:
- जीत — 42.43%
- पुश — 8.48%
- हानि — 49.09%
आइए हम बराबरी की स्थिति को नजरअंदाज कर दें, क्योंकि हमें जीत की संभावना 46.36% मिलेगी, बशर्ते कि हाथ शुद्ध जीत या हार में हल हो जाए।
आइए खेलने की गति के रूप में प्रति घंटे 100 हाथों का उपयोग करें।
हम लगातार कम से कम 60 हाथों की एक श्रृंखला देखने की संभावना का अनुमान इस प्रकार लगा सकते हैं:
100×12×0.4636 60 = 89,412,355,233,588,500 में 1.तुलना के आधार पर, यदि आपने पावरबॉल और एक मेगामिलियंस टिकट खरीदा है, तो दोनों जीतने की संभावना 88,412,922,115,818,300 में 1 होगी।
इसलिए 12 घंटे के खेल में लगातार 60 लॉटरी जीतने की तुलना में दोनों लॉटरी जीतने की संभावना थोड़ी अधिक होगी।


