जादूगर से पूछो #352
मिसिसिपी स्टड में अधिकतम भुगतान से हाउस एज में कितनी वृद्धि होती है?
अच्छा सवाल। मिसिसिपी स्टड खिलाड़ियों को निश्चित रूप से पता होना चाहिए कि अधिकतम भुगतान रॉयल फ्लश पर उनकी जीत को कम कर सकता है, जिससे हाउस एज बढ़ जाता है।
मिसिसिपी स्टड में रॉयल फ्लश के लिए अधिकतम भुगतान 500 से 1 है और यह सभी दांवों पर लागू होता है। खिलाड़ी के पास अपने एंटे के 3 गुना तक दांव बढ़ाने के दो मौके होते हैं, इसलिए उसका अंतिम दांव उसके एंटे के 7 गुना तक हो सकता है। अगर खिलाड़ी को रॉयल की उम्मीद है, तो उसे अधिकतम दांव लगाना चाहिए।
मिसिसिपी स्टड में, भुगतान सीमा से प्रभावित हुए बिना, खिलाड़ी को एंटे पर अधिकतम 3500/3500 का दांव लगाना चाहिए। उदाहरण के लिए, यदि अधिकतम भुगतान $80,000 है, तो मैं एंटे पर अधिकतम $22.86 का दांव लगाने की सलाह देता हूँ। मैं इसे $20 तक पूर्णांकित करूँगा।
निम्नलिखित तालिका विभिन्न दांवों पर हाउस एज और सामान्य अधिकतम जीत दर्शाती है। यह तालिका जीत की कोई सीमा नहीं रखते हुए इष्टतम खिलाड़ी रणनीति मानती है। ध्यान दें कि दांव का आकार बढ़ने और सीमा घटने के साथ हाउस एज कैसे बढ़ता है।
भुगतान सीमा के साथ हाउस एज
| शर्त | $50,000 की सीमा | $80,000 कैप | $100,000 कैप |
|---|---|---|---|
| $15 | 5.02% | 4.91% | 4.91% |
| $20 | 5.15% | 4.91% | 4.91% |
| $25 | 5.22% | 5.04% | 4.91% |
| $50 | 5.38% | 5.28% | 5.22% |
| $75 | 5.49% | 5.37% | 5.33% |
| $100 | 5.64% | 5.41% | 5.38% |
यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।
वाइटल वेगास ने एक खिलाड़ी को $1.1 मिलियन के जैकपॉट पर सिर्फ़ $200 की टिप देने के लिए फटकार लगाई है। ऐसी स्थिति में टिप देने का उचित शिष्टाचार क्या है?
हां, जहां वे खिलाड़ी को छोटी टिप के लिए फटकार लगाते हैं, वहीं वे इस सवाल को आसानी से टाल देते हैं कि उचित टिप कितनी होनी चाहिए।
न सिर्फ़ बड़े जैकपॉट के लिए टिप देने का तरीका ठीक से परिभाषित नहीं है, बल्कि छोटे जैकपॉट के लिए भी यह ठीक से परिभाषित नहीं है। इस बारे में अलग-अलग राय हैं, और ज़्यादातर राय ऐसे लोगों की हैं जिन्होंने कभी जैकपॉट नहीं जीता।
सबसे पहले, मैं इस बात पर ज़ोर देना चाहूँगा कि टिप देना वैकल्पिक नहीं है। कसीनो में, जीती गई राशि और सेवा के स्तर के अनुसार, आपको मिलने वाली सेवा के लिए टिप देना अपेक्षित होता है। इस बिंदु पर मिस्टर पिंक बनना और यह तर्क देना आसान है कि उन्हें किसी भी चीज़ के लिए टिप क्यों नहीं देनी चाहिए। टिप देना निश्चित रूप से एक दोषपूर्ण प्रणाली है, लेकिन हमारे यहाँ यही प्रणाली है। अगर आप सहमत नहीं हैं और टिप देने से इनकार करते हैं, तो उस सेवा के लिए न पूछें जिसके लिए टिप देने की अपेक्षा की जाती है।
दूसरा, एक बार यह तय हो जाने के बाद कि खिलाड़ी को जैकपॉट के लिए टिप देनी है, कितनी? मैं इस चर्चा को उस स्थिति तक सीमित रख रहा हूँ जहाँ खिलाड़ी सिर्फ़ एक जैकपॉट जीतता है। अगर खिलाड़ी कई जैकपॉट जीतता है, तो नियम अलग होते हैं, जो कि बहुत ऊँचे दांव पर सामान्य है। याद रखें, जैकपॉट की कागजी कार्रवाई के नियम ये हैं:
- "स्लॉट्स" पर $1,200 या अधिक की जीत।
- केनो में $1,500 या उससे अधिक की जीत।
- एक पोकर टूर्नामेंट में $5,000 या उससे अधिक की जीत।
- टेबल गेम में $600 या उससे अधिक की जीत और कम से कम 300 गुना दांव।
मैं टिप देने की क्या सलाह दूँ? पहले मैंने जैकपॉट का 0.5% से 2% तक कहा था, जैकपॉट जितना बड़ा होगा, प्रतिशत उतना ही कम होगा। हालाँकि, उस समय मैं इतने बड़े जैकपॉट के बारे में नहीं सोच रहा था। मुझे लगता है कि यह सीमा लगभग $100,000 तक उपयुक्त है।
इस सवाल ने मुझे एक खास फॉर्मूला बनाने पर मजबूर कर दिया है, जो मुझे लगता है कि $1200 से लेकर लाखों तक के किसी भी जैकपॉट के लिए उपयुक्त है। ये रहा:
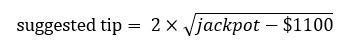
यदि आप छवि नहीं देख पा रहे हैं, तो यह 2×sqrt(जैकपॉट-$1100) है।
यहां कुछ सामान्य जैकपॉट राशियों के लिए सूत्र दिया गया है।
सुझाई गई टिप तालिका
| जैकपोट | बख्शीश |
|---|---|
| $1,200 | $20 |
| $2,000 | $60 |
| $5,000 | $125 |
| $10,000 | $189 |
| $20,000 | $275 |
| $50,000 | $442 |
| $100,000 | $629 |
| $1,000,000 | $1,999 |
$1.1 मिलियन के मामले में, मेरा फ़ॉर्मूला $2,096.57 सुझाता है। मुझे लगता है कि इसे $2,000 तक पूर्णांकित करना ठीक रहेगा। बेशक, सेवा की गुणवत्ता जैसे अन्य कारकों पर भी विचार करें।
यह प्रश्न विज़ार्ड ऑफ़ वेगास में मेरे मंच पर उठाया गया है और इस पर चर्चा की गई है।
किसी भी बड़ी संख्या के लिए, उस संख्या के निकट अभाज्य संख्याओं के बीच औसत दूरी क्या है? साथ ही, उस संख्या से छोटी कितनी अभाज्य संख्याएँ हैं?
किसी भी बड़ी संख्या n के निकट अभाज्य संख्याओं के बीच औसत दूरी का एक बहुत अच्छा अनुमान ln(n) है। यह उल्लेखनीय है कि यह अनुमानक कितना अच्छा है।
प्रमाण के तौर पर, निम्न तालिका दस लाख के समूहों में पहले 15 मिलियन अभाज्य संख्याओं का परिसर दर्शाती है। यह तालिका अभाज्य संख्याओं के बीच परिसर में औसत दूरी और औसत दूरी के अनुमान को दर्शाती है। यह अनुमान परिसर में सबसे बड़े और सबसे छोटे अभाज्य संख्याओं के औसत का प्राकृतिक लघुगणक है। उदाहरण के लिए, दस लाख अभाज्य संख्याओं के 15वें समूह के लिए, यह ln((256,203,221+275,604,541)/2) है।
अभाज्य संख्याओं के बीच औसत दूरी
| प्रथम प्रधान सीमा में | अंतिम प्राइम सीमा में | अभाज्य सीमा में | औसत दूरी | अनुमान लगाना | |
|---|---|---|---|---|---|
| 2 | 15,485,863 | 1,000,000 | 15.485861 | 15.86229105 | |
| 15,485,867 | 32,452,843 | 1,000,000 | 16.966976 | 16.9922867 | |
| 32,452,867 | 49,979,687 | 1,000,000 | 17.52682 | 17.53434381 | |
| 49,979,693 | 67,867,967 | 1,000,000 | 17.888274 | 17.89175615 | |
| 67,867,979 | 86,028,121 | 1,000,000 | 18.160142 | 18.15864108 | |
| 86,028,157 | 104,395,301 | 1,000,000 | 18.367144 | 18.3716137 | |
| 104,395,303 | 122,949,823 | 1,000,000 | 18.55452 | 18.54883262 | |
| 122,949,829 | 141,650,939 | 1,000,000 | 18.70111 | 18.70058553 | |
| 141,650,963 | 160,481,183 | 1,000,000 | 18.83022 | 18.83322787 | |
| 160,481,219 | 179,424,673 | 1,000,000 | 18.943454 | 18.95103217 | |
| 179,424,691 | 198,491,317 | 1,000,000 | 19.066626 | 19.05703535 | |
| 198,491,329 | 217,645,177 | 1,000,000 | 19.153848 | 19.15337672 | |
| 217,645,199 | 236,887,691 | 1,000,000 | 19.242492 | 19.24163365 | |
| 236,887,699 | 256,203,161 | 1,000,000 | 19.315462 | 19.32305683 | |
| 256,203,221 | 275,604,541 | 1,000,000 | 19.40132 | 19.39864545 |
स्रोत: प्राइम पेज पर प्राइम्स के बीच का अंतराल ।
किसी भी दी गई संख्या के अंतर्गत अभाज्य संख्याओं की संख्या ज्ञात करने के लिए, हम ln(n) के औसत दूरी अनुमान को एकीकृत करके शुरुआत कर सकते हैं। इससे हमें किसी भी संख्या n तक के अभाज्य संख्याओं के बीच की औसत दूरियों का योग प्राप्त होगा।
f(n)=ln(n) का समाकल क्या है? याद कीजिए कि भागों द्वारा एकीकरण हमें बताता है:
f(n)*g'(n) dn का समाकल = f(n)*g(n) - (f'(n)*g(n)) dn का समाकल
मान लीजिए f(n)=ln(n) और g'(n)=1. तो f'(n)=1/n और g(n)=n. इस प्रकार ln(n) का समाकल ln(n)*n - ((1/n)*n) का समाकल = ln(n)*n - n = n*(ln(n)-1) होगा।
यदि हम n*(ln(n)-1) को n से भाग दें, तो हमें 2 से n तक की संख्याओं के परिसर के लिए अभाज्य संख्याओं के बीच की औसत दूरी प्राप्त होती है। यह ln(n)-1 है।
यदि हम n को अभाज्य संख्याओं के बीच की इस औसत दूरी से विभाजित करते हैं, तो हमें n के अंतर्गत अभाज्य संख्याओं की औसत संख्या प्राप्त होती है, जो n/(ln(n)-1) के बराबर होती है।
प्रमाण के तौर पर, नीचे दी गई तालिका विभिन्न बड़ी संख्याओं के अंतर्गत अभाज्य संख्याओं की संख्या और अनुमानित मान दर्शाती है। कृपया 15 सार्थक अंकों की सटीकता को क्षमा करें, जो कि एक्सेल में संभव नहीं है। कृपया कोई ऐसी स्प्रेडशीट बनाएँ जो इससे ज़्यादा अंकों को संभाल सके।
अभाज्य संख्याओं के बीच औसत दूरी
| एन | n से कम अभाज्य संख्याएँ | एन/(एलएन(एन)-1) |
|---|---|---|
| 10 | 4 | 8 |
| 100 | 25 | 28 |
| 1,000 | 168 | 169 |
| 10,000 | 1,229 | 1,218 |
| 100,000 | 9,592 | 9,512 |
| 1,000,000 | 78,498 | 78,030 |
| 10,000,000 | 664,579 | 661,459 |
| 100,000,000 | 5,761,455 | 5,740,304 |
| 1,000,000,000 | 50,847,534 | 50,701,542 |
| 10,000,000,000 | 455,052,511 | 454,011,971 |
| 100,000,000,000 | 4,118,054,813 | 4,110,416,301 |
| 1,000,000,000,000 | 37,607,912,018 | 37,550,193,650 |
| 10,000,000,000,000 | 346,065,536,839 | 345,618,860,221 |
| 100,000,000,000,000 | 3,204,941,750,802 | 3,201,414,635,781 |
| 1,000,000,000,000,000 | 29,844,570,422,669 | 29,816,233,849,001 |
| 10,000,000,000,000,000 | 279,238,341,033,925 | 279,007,258,230,820 |
| 100,000,000,000,000,000 | 2,623,557,157,654,230 | 2,621,647,966,812,030 |
| 1,000,000,000,000,000,000 | 24,739,954,287,740,800 | 24,723,998,785,920,000 |
| 10,000,000,000,000,000,000 | 234,057,667,276,344,000 | 233,922,961,602,470,000 |
| 100,000,000,000,000,000,000 | 2,220,819,602,560,910,000 | 2,219,671,974,013,730,000 |
| 1,000,000,000,000,000,000,000 | 21,127,269,486,018,700,000 | 21,117,412,262,910,000,000 |
| 10,000,000,000,000,000,000,000 | 201,467,286,689,315,000,000 | 201,381,995,844,660,000,000 |
| 100,000,000,000,000,000,000,000 | 1,925,320,391,606,800,000,000 | 1,924,577,459,166,810,000,000 |
| 1,000,000,000,000,000,000,000,000 | 18,435,599,767,349,200,000,000 | 18,429,088,896,563,900,000,000 |
| 10,000,000,000,000,000,000,000,000 | 176,846,309,399,143,000,000,000 | 176,788,931,049,964,000,000,000 |
स्रोत: प्राइम पेज पर कितने प्राइम हैं?


