WOO logo

विज़ार्ड अनुशंसा करता है

जादूगर से पूछो #349

निम्नलिखित आरेख में, नीले क्षेत्र का क्षेत्रफल क्या है?

गुमनाम

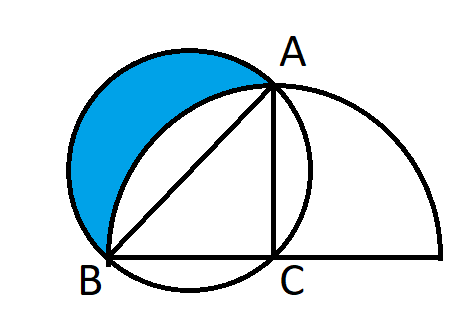
उत्तर के लिए नीचे दिए गए बटन पर क्लिक करें।

1/2

यहाँ मेरा समाधान (पीडीएफ) है।

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

वीडियो पोकर में ड्रॉ के बाद रखे गए कार्डों की औसत संख्या क्या है?

गुमनाम

निम्नलिखित तालिका 10 विभिन्न खेलों और भुगतान तालिकाओं में रखे गए कार्डों की औसत संख्या दर्शाती है। सूचीबद्ध खेलों का औसत 2.05 है।

वीडियो पोकर में रखे गए औसत कार्ड

खेल वेतन तालिका वापस करना Ave. कार्ड आयोजित
बोनस ड्यूस 10-4-3-3 97.36% 1.845550
ड्यूस वाइल्ड 25-15-9-5-3 100.76% 1.926010
व्हाइट हॉट एसेस 9-5 99.57% 2.055630
सुपर डबल डबल बोनस 7-5 99.17% 2.057280
डबल डबल बोनस 9-5 97.87% 2.058390
ट्रिपल डबल बोनस 8-5 95.97% 2.072620
बोनस पोकर 8-5 99.17% 2.080610
जैक्स या बेहतर 9-5 98.45% 2.081030
बोनस पोकर डीलक्स 8-5 97.40% 2.150470
दोहरा बोनस 9-6-5 97.81% 2.173550

शतरंज प्रतियोगिता में, प्रत्येक प्रतियोगी दूसरे प्रतियोगी के विरुद्ध एक मैच खेलता है। प्रत्येक प्रतियोगी को प्रत्येक जीत पर 1 अंक, प्रत्येक बराबरी पर 0.5 अंक और प्रत्येक हार पर 0 अंक मिलते हैं।

टूर्नामेंट के अंत में यह देखा गया कि सभी प्रतियोगियों को अलग-अलग अंक मिले तथा स्कोर रैंकिंग में अंतिम प्रतियोगी ने शीर्ष तीन प्रतियोगियों में से प्रत्येक को हराया।

तदनुसार, टूर्नामेंट में भाग लेने वाले प्रतियोगियों की न्यूनतम संख्या क्या है?

Gialmere

13

[स्पॉइलर=समाधान]

आइए खिलाड़ियों की संख्या को n कहें।

मेरा अनुमान है कि आखिरी स्थान पर रहने वाले खिलाड़ी ने शीर्ष 3 खिलाड़ियों के खिलाफ केवल तीन जीत हासिल की हैं, और बाकी सभी मैच हारे हैं। इससे उसे 3 अंक मिलते हैं।

फिर मैं हर अगले खिलाड़ी को अंकों के क्रम में पिछले खिलाड़ी से 0.5 अंक ज़्यादा अंक के रूप में गिनता हूँ। इससे सबसे ऊँची रैंकिंग वाले खिलाड़ी को 3+(n-1)/2 अंक मिलेंगे।

3 से 3+(n-1)/2 का योग, प्रति चरण 1/2 अंक लेने पर हमें (((n+5)*(n+6)/2)-15)/2 प्राप्त होता है।

n खिलाड़ियों के साथ खेले गए कुल खेल n*(n-1)/2 होते हैं, जहाँ हर कोई एक-दूसरे के साथ एक-एक बार खेलता है। प्रत्येक खेल में कुल एक अंक मिलता है, जो सभी खिलाड़ियों द्वारा अर्जित कुल अंकों के बराबर होता है।

फिर n के लिए हल करें:

(((एन+5)*(एन+6)/2)-15)/2 = एन*(एन-1)/2
((एन+5)*(एन+6)/2)-15 = एन*(एन-1)
(एन+5)*(एन+6)/2 = एन*(एन-1) + 15
(एन+5)*(एन+6) = 2*एन*(एन-1) + 30
n^2 + 11n + 30 = 2n^2 - 2n + 30
एन^2 + 11एन = 2एन^2 - 2एन
एन + 11 = 2एन-2
एन=13

नीचे दी गई तालिका में यह कैसे हो सकता है, इसका एक तरीका दिया गया है। तालिका का मुख्य भाग सभी 78 खेलों के विजेता को दर्शाता है।

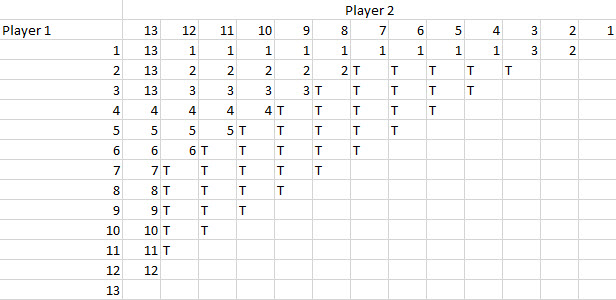
निम्नलिखित तालिका प्रत्येक खिलाड़ी के अंकों की संख्या दर्शाती है।

खिलाड़ी द्वारा कुल अंक

खिलाड़ी अंक
13 3
12 3.5
11 4
10 4.5
9 5
8 5.5
7 6
6 6.5
5 7
4 7.5
3 8
2 8.5
1 9
[/बिगाड़ने वाला]

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।