WOO logo

विज़ार्ड अनुशंसा करता है

जादूगर से पूछो #341

2 से 12 तक का योग प्राप्त करने के लिए दो पासों को कितनी बार उछालना चाहिए? कृपया अपने उत्तर के लिए कैलकुलस का प्रयोग करें।

BruceZ

लगभग 61.2173847639572 रोल.

[स्पॉइलर=समाधान]

याद रखें कि कुल 2 रोल आने की प्रायिकता 1/36 है। t रोल में, कुल 2 रोल आने की अपेक्षित प्रायिकता t/36 है। मान लें कि रोल के बीच का समय t/36 के माध्य के साथ चरघातांकी रूप से वितरित है। पॉइसन वितरण हमें बताता है कि कुल 2 रोल आने पर शून्य रोल आने की प्रायिकता exp(-t/36) है।

याद कीजिए कि कुल 3 आने की प्रायिकता 2/36 = 1/18 है। इसी तर्क से, पॉइसन वितरण हमें बताता है कि कुल 3 आने पर शून्य आने की प्रायिकता exp(-t/18) है।

याद कीजिए कि कुल 4 आने की प्रायिकता 3/36 = 1/12 है। इसी तर्क से, पॉइसन वितरण हमें बताता है कि कुल 4 आने पर शून्य आने की प्रायिकता exp(-t/12) है।

याद कीजिए कि कुल 5 आने की प्रायिकता 4/36 = 1/9 है। इसी तर्क से, पॉइसन वितरण हमें बताता है कि कुल 5 आने पर शून्य आने की प्रायिकता exp(-t/9) है।

याद कीजिए कि कुल 6 आने की प्रायिकता 5/36 है। इसी तर्क से, पॉइसन वितरण हमें बताता है कि कुल 6 आने पर शून्य आने की प्रायिकता exp(-5t/36) है।

याद कीजिए कि कुल 7 आने की प्रायिकता 6/36 = 1/6 है। इसी तर्क से, पॉइसन वितरण हमें बताता है कि कुल 7 आने पर शून्य आने की प्रायिकता exp(-t/6) है।

8 से 12 के लिए संभावनाएं 2 से 6 के लिए समान हैं।

इस प्रकार, संभावना है कि प्रत्येक कुल की t इकाइयों में कम से कम एक बार रोल किया गया है:

(1-एक्सप(-t/36))^2 * (1-एक्सप(-t/18))^2 * (1-एक्सप(-t/12))^2 * (1-एक्सप(-t/9))^2 * (1-एक्सप(-5t/36))^2 * (1-एक्सप(-t/6))

कम से कम कुल समय की t इकाइयों में रोल न किए जाने की संभावना 1 है - (1-exp(-t/36))^2 * (1-exp(-t/18))^2 * (1-exp(-t/12))^2 * (1-exp(-t/9))^2 * (1-exp(-5t/36))^2 * (1-exp(-t/6))

कम से कम एक कुल के बिना अपेक्षित समय प्राप्त करने के लिए हम उपरोक्त फ़ंक्शन को 0 से अनंत तक एकीकृत करते हैं।

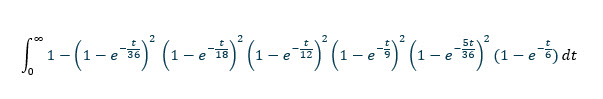
एक इंटीग्रल कैलकुलेटर (मैं इसकी अनुशंसा करता हूं) इसे आसानी से हल कर देगा क्योंकि 769767316159/12574325400 = लगभग 61.2173847639572 रोल्स।

[/बिगाड़ने वाला]

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

दो पासे, एक लाल और एक नीला, बार-बार घुमाएँ। हर पासे के घुमावों का योग ध्यान में रखें। जब तक इन दोनों का संचयी योग बराबर न हो जाए, तब तक कितनी बार घुमावों की अपेक्षित संख्या होगी?

teliot

उत्तर अनंत है।

[spoiler=अधिक टिप्पणियाँ]

यह समझाना मुश्किल है कि उत्तर अनंत क्यों है। बात को और भी उलझाने वाली और विरोधाभासी बनाने के लिए, कुल योग के बराबर होने की संभावना 1 है।

निम्नलिखित तालिका 1 से 16 रोल के बाद पहली बार कुल योग समान होने की संभावना दर्शाती है।

पहली बार समान योग की संभावना

रोल्स संभावना
1 0.166667
2 0.112654
3 0.092850
4 0.080944
5 0.072693
6 0.066539
7 0.061722
8 0.057819
9 0.054573
10 0.051819
11 0.049443
12 0.047367
13 0.045532
14 0.043895
15 0.042423
16 0.041089

एक्सेल इस वक्र के बहुत करीब फिट को y = 0.1784*x-1.011 दिखाता है, जहां x = रोल की संख्या और y = संभावना है।

इस अनंत श्रृंखला का योग अनंत है।

[/बिगाड़ने वाला]

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

पेन्सिलवेनिया कैश 5 गेम का ब्रेक-ईवन जैकपॉट क्या है? आप टैक्स और जैकपॉट शेयरिंग को नज़रअंदाज़ कर सकते हैं।

100xOdds

सबसे पहले, नियमों पर गौर करते हैं। दांव की कीमत $2 है। यह खेल 43 में से पाँच गेंदें निकालने पर आधारित है। भुगतान तालिका इस प्रकार है:

  • मैच 5 = जैकपॉट
  • गणित 4 = $200
  • मैच 3 = $10
  • मैच 2 = $2

इसके अलावा, मुझे लगता है कि खिलाड़ी को एक स्क्रैच-ऑफ कार्ड मिलता है। इसमें $6 जीतने की 1/80 संभावना और $2 जीतने की 1/5 संभावना होती है।

नीचे दी गई तालिका मेरे द्वारा मूल खेल के विश्लेषण को दर्शाती है। इसमें 2 से 4 संख्याओं को पकड़ने का मूल्य $0.287784 है।

नकद 5 वापसी तालिका

पकड़ना भुगतान करता है युग्म संभावना वापस करना
5 खजाना 1 0.000001 ?
4 200 190 0.000197 0.039477
3 10 7030 0.007303 0.073032
2 2 84360 0.087638 0.175276
1 0 369075 0.383416 0.000000
0 0 501942 0.521445 0.000000
कुल 0 962598 1.000000 0.287784

नीचे दी गई तालिका क्विक कैश इंस्टेंट विन फ़ीचर पर मेरे विश्लेषण को दर्शाती है। निचले दाएँ सेल में $0.475 का मान दर्शाया गया है।

तत्काल नकद वापसी तालिका

पकड़ना भुगतान करता है संभावना वापस करना
6 1 0.012500 0.075000
2 16 0.200000 0.400000
0 63 0.787500 0.000000
कुल 80 1.000000 0.475000

इस प्रकार, गैर-प्रगतिशील पुरस्कारों का मूल्य $0.287784 + $0.475000 = $0.762784 है।

मान लीजिए j, ब्रेक-ईवन जैकपॉट के मान के बराबर है। तो:

2 = 0.762784 + जे × (1/962598)
1.237216 = जे × (1/962598)
जे = 1.237216 × 962598
जे = $1,190,941.95.

जैकपॉट में प्रत्येक $100,000 के लिए कुल रिटर्न दर 0.381392 प्लस 0.051943 है।

जैसा कि प्रश्न में कहा गया है, यह सब करों और जैकपॉट बंटवारे की अनदेखी करता है।

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।