WOO logo

विज़ार्ड अनुशंसा करता है

जादूगर से पूछो #340

यदि किसी कैसीनो ने टाई बेट पर जीत को सामान्य 8 से 1 से बढ़ाकर 9 से 1 कर दिया, तो समान अपेक्षित जीत के लिए टाई पर कितने अतिरिक्त दांव लगाने की आवश्यकता होगी?

dandolos2000

बैकारेट में बराबरी की संभावना 0.095155968 है।

8 से 1 की सामान्य जीत पर, खिलाड़ी को अपेक्षित वापसी 0.095156 × (8+1) - 1 = -0.143596 है।

9 से 1 की जीत पर, खिलाड़ी को अपेक्षित वापसी 0.095156 × (9+1) - 1 = --0.048440 है।

8 से 1 की जीत पर अपेक्षित खिलाड़ी की हानि 0.143596/0.048440 = 2.9643960 गुना अधिक है। इस प्रकार, यदि अपेक्षित कैसीनो जीत समान रहे, तो कैसीनो को जीत को 9 से 1 तक बढ़ाने पर टाई पर 2.9643960 गुना अधिक कार्रवाई की आवश्यकता होगी।

यह प्रश्न विज़ार्ड ऑफ़ वेगास में मेरे मंच पर उठाया गया है और इस पर चर्चा की गई है।

मान लीजिए एक डिब्बे में 100 गेंदें हैं, जिन पर 1 से 100 तक की संख्या अंकित है। 10 गेंदें बिना प्रतिस्थापन के यादृच्छिक रूप से निकाली जाती हैं। निकाली गई सबसे छोटी गेंद की माध्य संख्या क्या है?

ThatDonGuy

निम्न तालिका संयोजनों की संख्या, प्रायिकता और सबसे कम गेंद (गेंद और प्रायिकता का गुणनफल) में योगदान दर्शाती है। निचले दाएँ कक्ष में अपेक्षित सबसे कम गेंद 9.1818182 दिखाई गई है।

सबसे कम गेंद

सबसे कम
गेंद		 युग्म संभावना अपेक्षित
लो बॉल
1 1,731,030,945,644 0.100000 0.100000
2 1,573,664,496,040 0.090909 0.181818
3 1,429,144,287,220 0.082560 0.247681
4 1,296,543,270,880 0.074900 0.299600
5 1,174,992,339,235 0.067878 0.339391
6 1,063,677,275,518 0.061448 0.368686
7 961,835,834,245 0.055564 0.388950
8 868,754,947,060 0.050187 0.401497
9 783,768,050,065 0.045278 0.407498
10 706,252,528,630 0.040800 0.407995
11 635,627,275,767 0.036720 0.403915
12 571,350,360,240 0.033006 0.396076
13 512,916,800,670 0.029631 0.385199
14 459,856,441,980 0.026565 0.371917
15 411,731,930,610 0.023785 0.356780
16 368,136,785,016 0.021267 0.340271
17 328,693,558,050 0.018988 0.322801
18 293,052,087,900 0.016929 0.304728
19 260,887,834,350 0.015071 0.286354
20 231,900,297,200 0.013397 0.267933
21 205,811,513,765 0.011890 0.249680
22 182,364,632,450 0.010535 0.231771
23 161,322,559,475 0.009319 0.214347
24 142,466,675,900 0.008230 0.197524
25 125,595,622,175 0.007256 0.181388
26 110,524,147,514 0.006385 0.166007
27 97,082,021,465 0.005608 0.151425
28 85,113,005,120 0.004917 0.137673
29 74,473,879,480 0.004302 0.124766
30 65,033,528,560 0.003757 0.112708
31 56,672,074,888 0.003274 0.101491
32 49,280,065,120 0.002847 0.091100
33 42,757,703,560 0.002470 0.081512
34 37,014,131,440 0.002138 0.072701
35 31,966,749,880 0.001847 0.064634
36 27,540,584,512 0.001591 0.057276
37 23,667,689,815 0.001367 0.050589
38 20,286,591,270 0.001172 0.044534
39 17,341,763,505 0.001002 0.039071
40 14,783,142,660 0.000854 0.034160
41 12,565,671,261 0.000726 0.029762
42 10,648,873,950 0.000615 0.025837
43 8,996,462,475 0.000520 0.022348
44 7,575,968,400 0.000438 0.019257
45 6,358,402,050 0.000367 0.016529
46 5,317,936,260 0.000307 0.014132
47 4,431,613,550 0.000256 0.012032
48 3,679,075,400 0.000213 0.010202
49 3,042,312,350 0.000176 0.008612
50 2,505,433,700 0.000145 0.007237
51 2,054,455,634 0.000119 0.006053
52 1,677,106,640 0.000097 0.005038
53 1,362,649,145 0.000079 0.004172
54 1,101,716,330 0.000064 0.003437
55 886,163,135 0.000051 0.002816
56 708,930,508 0.000041 0.002293
57 563,921,995 0.000033 0.001857
58 445,891,810 0.000026 0.001494
59 350,343,565 0.000020 0.001194
60 273,438,880 0.000016 0.000948
61 211,915,132 0.000012 0.000747
62 163,011,640 0.000009 0.000584
63 124,403,620 0.000007 0.000453
64 94,143,280 0.000005 0.000348
65 70,607,460 0.000004 0.000265
66 52,451,256 0.000003 0.000200
67 38,567,100 0.000002 0.000149
68 28,048,800 0.000002 0.000110
69 20,160,075 0.000001 0.000080
70 14,307,150 0.000001 0.000058
71 10,015,005 0.000001 0.000041
72 6,906,900 0.000000 0.000029
73 4,686,825 0.000000 0.000020
74 3,124,550 0.000000 0.000013
75 2,042,975 0.000000 0.000009
76 1,307,504 0.000000 0.000006
77 817,190 0.000000 0.000004
78 497,420 0.000000 0.000002
79 293,930 0.000000 0.000001
80 167,960 0.000000 0.000001
81 92,378 0.000000 0.000000
82 48,620 0.000000 0.000000
83 24,310 0.000000 0.000000
84 11,440 0.000000 0.000000
85 5,005 0.000000 0.000000
86 2,002 0.000000 0.000000
87 715 0.000000 0.000000
88 220 0.000000 0.000000
89 55 0.000000 0.000000
90 10 0.000000 0.000000
91 1 0.000000 0.000000
कुल 17,310,309,456,440 1.000000 9.181818

इस तरह के प्रश्नों को हल करने का एक आसान तरीका है, जहाँ सबसे छोटी गेंद 1 है। सबसे छोटी गेंद का सूत्र (m+1)/(b+1) है, जहाँ m गेंद का अधिकतम मान है और b गेंदों की संख्या है। इस स्थिति में, m=100 और n=10 है, इसलिए सबसे छोटी गेंद 101/11 = 9.181818 है।

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

निम्नलिखित पहेली 6 मार्च, 2021 के न्यूयॉर्क टाइम्स में छपी।

नियम बहुत सरल हैं:

  1. प्रत्येक पंक्ति, स्तंभ और क्षेत्र में ठीक दो तारे होने चाहिए।
  2. कोई भी दो तारे एक दूसरे को स्पर्श नहीं कर सकते, तिरछे भी नहीं।

क्या आप समाधान में मदद कर सकते हैं?

गुमनाम

इसे "टू नॉट टच" पहेली कहते हैं। नीचे दिए गए बटन पर मेरा उत्तर और हल लिखा है।

[स्पॉइलर=उत्तर]

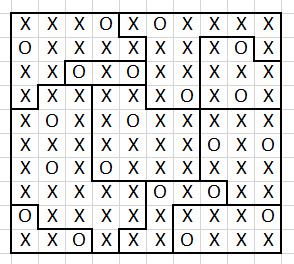
दो स्पर्श हल नहीं

[/बिगाड़ने वाला]

यहां मेरा समाधान (पीडीएफ) है।

एक निष्पक्ष छह-पक्षीय पासे के किसी एक पक्ष को छह बार घुमाने के लिए अपेक्षित रोलों की संख्या क्या है?

Ace2

मेरे उत्तर के लिए नीचे दिए गए बटन पर क्लिक करें।

उत्तर है 2597868106693535971 / 131621703842267136 = अनुमान: 19.73738396371749

यहां मेरा समाधान (पीडीएफ) है।