विज़ार्ड अनुशंसा करता है
-
$11000 स्वागत बोनस -
$3000 स्वागत बोनस -
$777 तक बोनस
जादूगर से पूछो #338
2 से 12 तक का कुल योग प्राप्त करने के लिए दो पासों को औसतन कितनी बार घुमाना पड़ेगा?
[स्पॉइलर=समाधान]
इसका उत्तर देने के लिए मार्कोव श्रृंखला का उपयोग किया जा सकता है, लेकिन मुझे कैलकुलस ज़्यादा पसंद है। मुख्य बात यह है कि यदि रोल के बीच का समय घातांकीय रूप से वितरित हो और माध्य एक हो, तो उत्तर वही होगा। अतः, उत्तर को 0 से अनंत तक के समाकलन के रूप में व्यक्त किया जा सकता है:
1-(1-एक्सप(-x/36))^2*(1-एक्सप(-x/18))^2*(1-एक्सप(-x/12))^2*(1-एक्सप(-x/9))^2*(1-एक्सप(-5*x/36))^2*(1-एक्सप(-x/6))
आप ऐसे समाकलों को समाकल कैलकुलेटर से आसानी से हल कर सकते हैं।
आप मेरी अपेक्षित परीक्षण कैलकुलेटर के साथ ऐसी किसी भी समस्या को हल कर सकते हैं।
[/बिगाड़ने वाला]एक वर्ग के बीच में एक चींटी है। वह ऊपरी बाएँ कोने से 17 इंच, ऊपरी दाएँ कोने से 20 इंच और निचले दाएँ कोने से 13 इंच की दूरी पर है।
wizardofodds.com /wizfiles/img/2212/ant_and_square.png">
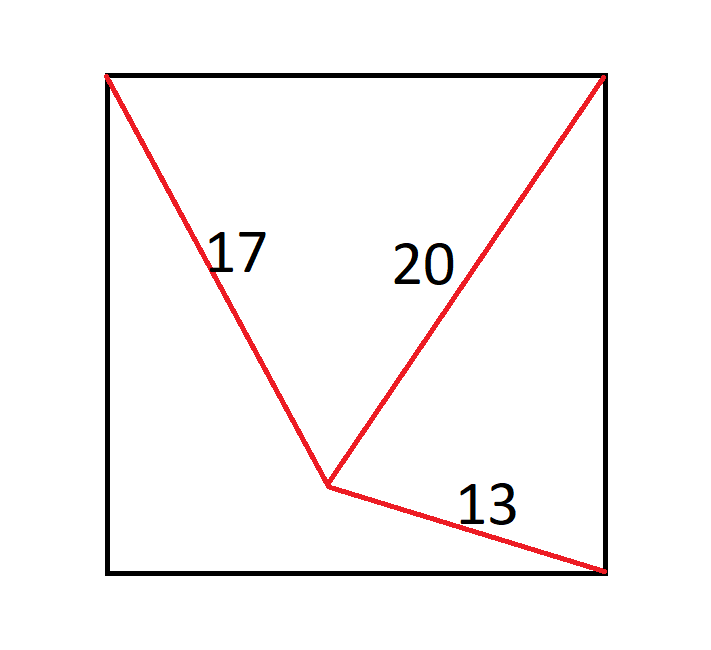
वर्ग कितना बड़ा है?
cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b)
[स्पॉइलर=समाधान]
सबसे पहले, त्रिभुज ABE को 90 डिग्री घुमाकर एक नया त्रिभुज BDF बनाएं।
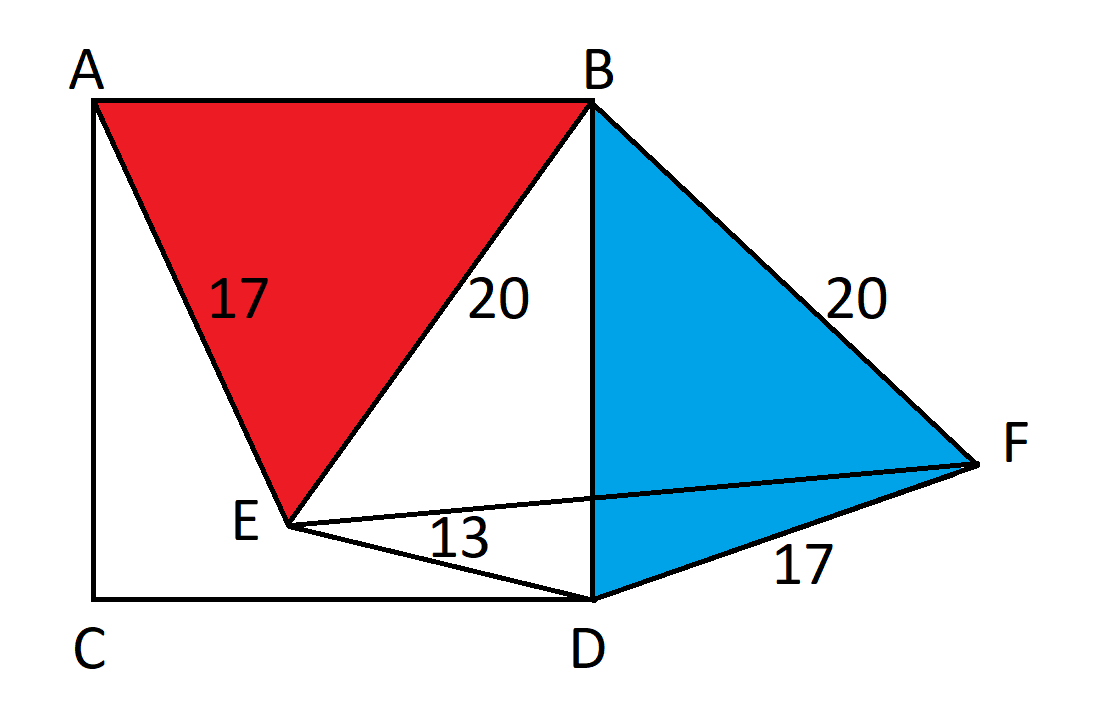
चूँकि त्रिभुज को 90 डिग्री घुमाया गया था, इसलिए परिभाषा के अनुसार कोण EBF = 90 है। पाइथागोरस सूत्र के अनुसार, EF = 20*sqrt(2)।
कोसाइन के नियम से: 17^2 = 13^2 + (20*sqrt(2))^2 - 2*13*20*sqrt(2)*cos(DEF).
289 = 169 + 800 - 520*sqrt(2)*cos(DEF)
520*sqrt(2)*cos(DEF) = 680.
cos(DEF) = 17*sqrt(2)/26.
याद करें, sin^2(x) + cos^2(x) = 1. आइए इसका उपयोग sin(DEF) को हल करने के लिए करें।
sin^2(DEF) + cos^2(DEF) = 1
sin^2(DEF) + (17*sqrt(2)/26)^2 = 1
sin^2(DEF) + 289/338 = 1
sin^2(DEF) = 49/338
sin(DEF) = 7*sqrt(2)/26
अब कोण BED पर विचार करें।
कोण BED = कोण BEF + कोण FED.
हम जानते हैं कि EBF 90 डिग्री का होता है और एक समद्विबाहु त्रिभुज है। इससे कोण BEF 45 डिग्री का हो जाएगा।
तो, कोण BED = 45 डिग्री + कोण FED.
याद करें, cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b).
cos(BED) = cos(BEF + FED) = cos(BEF)*cos(FED) - पाप(BEF)*sin(FED)
= (1/वर्ग(2))*17*वर्ग(2)/26 - (1/वर्ग(2))*7*वर्ग(2)/26
= (17/26) - (7/26) = 10/26 = 5/13
आइये कोसाइन के नियम को पुनः लागू करें, इस बार त्रिभुज BED पर।
बीडी^2 = 20^2 + 13^2 - 2*20*13*(5/13)
= 400 + 169 - 200 = 369
BD प्रश्नगत वर्ग की भुजा है, अतः BD^2 उस वर्ग का क्षेत्रफल है, जिसे हमने 369 दर्शाया है।
[/बिगाड़ने वाला]यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।
ड्रॉप डेड पाँच मानक पासों से खेला जाने वाला एक खेल है। आप अपनी बारी की शुरुआत सभी पाँच पासों को फेंककर करते हैं। अगर उनमें से कोई भी 2 या 5 नहीं आता है, तो आप पासों का योग करें, उस योग को अपने अंक में जोड़ें और फिर से फेंकें। अगर कोई 2 या 5 आता है, तो उस फेंके गए पासे का आपका स्कोर शून्य होता है। 2 या 5 दिखाने वाले सभी पासों को मृत घोषित कर दिया जाता है और अलग रख दिया जाता है। फिर आप बचे हुए पासों को फिर से फेंकते हैं। खेल आगे बढ़ता है, या तो आप अंक अर्जित करते हैं या पासे हटाते हैं। आपकी बारी तब समाप्त होती है जब आपके सभी पासे हटा दिए जाते हैं, जिसके बाद आपको ड्रॉप डेड घोषित कर दिया जाता है। आपके सभी स्कोरिंग पासों को जोड़कर आपका अंतिम अंक प्राप्त किया जाता है। सबसे ज़्यादा अंक जीतने वाला विजेता होता है।
इस खेल के लिए आपका अपेक्षित स्कोर क्या है?
[स्पॉइलर=समाधान]
आइए एक पासा शेष रहने पर परिदृश्य से शुरू करें और पीछे की ओर बढ़ें।
मान लीजिए चर a एक पासा शेष रहने पर अपेक्षित अतिरिक्त अंक है।
औसत रोल जो 2 या 5 नहीं है वह (1+3+4+6)/4 = 7/2 है।
ए = (2/3)×(ए + 7/2).
ए/3 = 7/3.
ए = 7.
अब, आइए b की गणना करें, जो कि दो पासे शेष रहने पर अपेक्षित अंक है।
बी = (2/3) 2 ×(बी + 2 × (7/2)) + 2×(2/3)×(1/3)×ए.
बी = 11.2.
अब, आइए c की गणना करें, जो कि तीन पासे शेष रहने पर अपेक्षित अंक है।
सी = (2/3) 3 ×(सी + 3× (7/2)) + 3×(2/3) 2 ×(1/3)×बी + 3×(2/3)×(1/3) 2 ×बी.
सी = 1302/95 = 13.705263.
अब, आइए d की गणना करें, जो कि चार पासे शेष रहने पर अपेक्षित अंक है।
डी = (2/3) 4 ×(डी + 4× (7/2)) + 4×(2/3) 3 ×(1/3)×सी + 6×(2/3) 2 ×(1/3) 2 ×बी + 4×(2/3)×(1/3) 3 ×ए.
डी = 3752/247 = 15.190283.
अंत में, आइए e की गणना करें, जो कि पांच पासे शेष रहने पर अपेक्षित अंक है।
ई = (2/3) 5 ×(ई + 5×(7/2)) + 5×(2/3) 4 ×(1/3)×डी + 10×(2/3) 3 ×(1/3) 2 ×सी + 10×(2/3) 2 ×(1/3) 3 ×बी + 5×(2/3)×(1/3) 4 ×ए।
ई = 16.064662.
यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।
[/बिगाड़ने वाला]थ्री कार्ड पोकर में पेयरप्लस बेट पर विचार करें, जो 1-4-6-30-40 पे टेबल का पालन करता है। हालाँकि, यह हुकुम के मिनी-रॉयल के लिए एक जैकपॉट और बाकी तीन सूट के मिनी-रॉयल के लिए उस जैकपॉट का 25% देता है। बेट के निष्पक्ष होने के लिए मीटर कितना ऊँचा होना चाहिए?
उत्तर शर्त राशि का 384 गुना है।
इसके ऊपर प्रत्येक अतिरिक्त 100 दांव के लिए, रिटर्न 0.79% बढ़ जाता है।
यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।