जादूगर से पूछो #336

यह खिलाड़ी के लिए अच्छा है! उनकी वेबसाइट पर विस्तार से जानकारी नहीं दी गई है, इसलिए मैं मान रहा हूँ कि यह सिर्फ़ शुरुआती दो कार्डों के लिए है। मैंने अक्टूबर 2018 के एक पुराने करंट ब्लैकजैक न्यूज़लेटर से देखा, ज़्यादातर टेबलों में ये नियम होते हैं:

• डीलर ने सॉफ्ट 17 मारा
• छह डेक
• ब्लैकजैक 3 से 2 का भुगतान करता है
• विभाजन के बाद डबल की अनुमति
• इक्कों को पुनः विभाजित करने की अनुमति है

मेरा ब्लैकजैक हाउस एज कैलकुलेटर कहता है कि इन नियमों में निरंतर शफलर के साथ 0.55% और कट कार्ड के साथ 0.57% हाउस एज है।

नियमों के बावजूद, पहले दो पत्तों में हार्ड 16 आने की संभावना 6.51% है। 6.51% संभावना के साथ $16 प्राप्त करना प्रति हाथ $1.04 के बराबर है। मैं न्यूनतम दांव $25 मान रहा हूँ क्योंकि कोरोनावायरस के इस दौर में ज़्यादातर कैसीनो अपनी न्यूनतम राशि बढ़ा रहे हैं। बोनस को छोड़कर, $25 के दांव पर प्रति हाथ अपेक्षित नुकसान $0.14 है। यानी प्रति हाथ अपेक्षित जीत $1.04 - $0.14 = $0.90 है। दांव की राशि के सापेक्ष, यह खिलाड़ी को 3.59% का लाभ देता है!

यदि हम $25 के तीन हाथों को 80 राउंड प्रति घंटे पर खेलने की अच्छी स्थिति में मानें, तो प्रति घंटे $216 की अपेक्षित जीत होगी!

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

[स्पॉइलर=समाधान]

सबसे पहले, खूंटियों के लिए combin(25,3) = 2,300 संभावित संयोजन हैं।

इनमें से कितने संयोजन मिलकर त्रिभुज बनाते हैं? आइए इस बोर्ड की मदद लें:

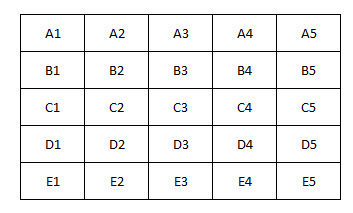
सबसे पहले, पाँच पंक्तियाँ, पाँच स्तंभ और दो विकर्ण हैं। इनमें से किसी एक के लिए, खूँटियों को एक पंक्ति में रखने के लिए संयोजन (5,3) = 10 तरीके हैं। इस प्रकार, 12*10 = 120 संयोजन हैं।

दूसरा, किसी पंक्ति/स्तंभ के मध्य वर्ग को आसन्न पंक्ति/स्तंभ के मध्य वर्ग से जोड़ने के चार तरीके हैं। दूसरे शब्दों में, ये तीन स्थान हैं:

• ए3, बी4, सी5
• सी5, डी4, ई3
• ई3, डी2, सी1
• सी1, बी2, ए3

तो, अब हम 120 + 4 = 124 पर हैं

तीसरा, चार अलग-अलग विकर्ण रेखाएँ हैं जो चार स्थान हैं:

• ए2, बी3, सी4, डी5
• बी5, सी4, डी3, ई2
• ई4, डी3, सी2, बी1
• डी1, सी2, बी3, ए4

उनमें से प्रत्येक के लिए तीन खूंटियाँ लगाने के combin(4,3)=4 तरीके हैं। तो इसमें 4*4 = 16 और जुड़ जाते हैं।

अब हम 124+16 = 140 पर हैं

चौथा, शतरंज में घोड़ों के 2x1 L आकार में चलने के तरीके पर विचार करें। प्रत्येक कोने के लिए घोड़ा दो तरह से चल सकता है। इन सभी में घोड़ा उसी पंक्ति में दोबारा चल सकता है जहाँ पहली चाल चली थी। यानी 4*2 = 8 और:

• ए1, सी2, ई3 ए1, बी3, सी5
• ए5, बी3, सी1
• ए5, सी4, ई3
• ई5, सी4, ए3
• ई5, डी3, सी1
• ई1, डी3, सी5
• ई1, सी2, ए3

चार ऐसी नाइट लाइनें भी हैं जो केंद्र से होकर जाती हैं:

• ए2, सी3, ई4
• ए4, सी3, ई2
• बी5, सी3, डी1
• डी5, सी3, बी1

12 नाइट लाइनों को जोड़ने पर, हम 140+12= 152 पर हैं

यदि कुल 2,300 संयोजन हैं और 152 रेखाएँ बनाते हैं, तो 2300-152 = 2,148 रेखाएँ नहीं बनाते हैं और इस प्रकार त्रिभुज बनाते हैं।

इस प्रकार, हमारा उत्तर 2,148/2,300 = 93.39% है।

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।

सरलता के लिए, मान लें कि इक्कों को दोबारा बाँटने की अनुमति नहीं है। यह भी याद रखें कि स्पैनिश 21 में 48 पत्तों वाले स्पैनिश डेक का इस्तेमाल होता है, जिनमें 10 नहीं होते। अंत में, याद रखें कि स्पैनिश 21 में 21 अंक स्वतः विजेता होते हैं।

इस नियम के बिना भी, खिलाड़ी को हमेशा इक्कों को बाँटना चाहिए। चार स्पैनिश डेक वाले खेल में इक्कों का एक जोड़ा मिलने की संभावना कॉम्बिन(16,2)/कॉम्बिन(192,2) = 120/18336 = 0.65% है।

प्रत्येक इक्के के 10 आने की संभावना (4*12)/(48*12-2) = 48/190 = 25.26% है। दो इक्कों के साथ, ब्लैकजैक में बदलने वाली अपेक्षित संख्या 2*48/190 = 96/190 = 0.5053 है।

प्रत्येक ब्लैकजैक का मूल्य एक अतिरिक्त आधी इकाई होगा। इस प्रकार, इस नियम का मान (120/18336)*(96/190)*(1/2) = 0.17% है।

इस नियम के साथ भी, खिलाड़ी को दहाई का बंटवारा नहीं करना चाहिए, इसलिए हमें इसकी चिंता करने की ज़रूरत नहीं है। इस प्रकार, यह नियम हाउस एज को 0.17% कम कर देता है।

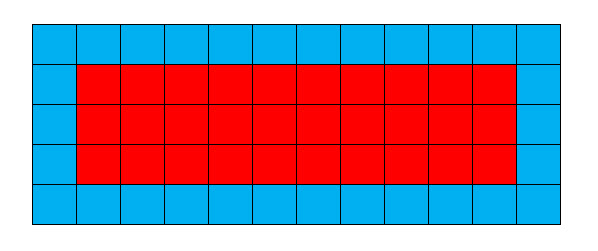
[स्पॉइलर=समाधान]

मान लीजिए x और y आंतरिक आयत के आयाम हैं।

उस आयत का क्षेत्रफल x*y है।

परिमाप का क्षेत्रफल 2x + 2y + 4 है

यह दिया गया है कि xy = 2x+2y+4

xy-2x = 2y + 4

x(y-2) = 2y+4

x=(2y+4)/(y-2)

y का मान 3 से अधिक या बराबर होना चाहिए। आइए देखें कि 3 के बराबर या उससे अधिक y मानों के लिए x क्या है।

यदि y = 3, तो x = 10
यदि y = 4, तो x = 6
यदि y = 5, तो x = 14/3
यदि y = 6, तो x=4

तो, 3x10 और 4x6 हल हैं। 6x4 हल नहीं है, क्योंकि यह एक अद्वितीय हल नहीं है। जैसे-जैसे y बड़ा होता जाएगा, x छोटा होता जाएगा। जैसे y का मान 3 के बराबर या उससे बड़ा होना चाहिए, वैसे ही x का भी होना चाहिए। y के बढ़ने के साथ-साथ x का मान भी घटता जाता है, इसलिए x का केवल एक ही संभावित मान है, जो x=3 है। हालाँकि, यदि x=3 है, तो y=10 है, और वह भी अद्वितीय नहीं है।

तो उत्तर 2 है: आंतरिक आयत के लिए 3x10 और 4x6। यदि आप बाहरी आयत के अनुसार हल गिनना पसंद करते हैं, तो वे 5x12 और 6x8 होंगे।

यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।