WOO logo

विज़ार्ड अनुशंसा करता है

जादूगर से पूछो #335

मैंने विज़ार्ड ऑफ़ वेगास में आपके लेख में 105.22% रिटर्न वाले रिवर्सिबल रॉयल गेम के बारे में पढ़ा। यह रिटर्न कार्ड ऑर्डर सहित, सर्वोत्तम रणनीति को ध्यान में रखकर बनाया गया है। अगर मैं औसत रॉयल जीत मान लूँ तो रिटर्न कितना होगा? अगर मैं साधारण 6-5 बोनस पोकर रणनीति अपनाऊँ, जो कि आधार भुगतान तालिका है, तो क्या होगा?

गुमनाम

यह मानते हुए कि कोई रणनीति विचलन नहीं है, 60 में से 1 रॉयल क्रमिक होगा। प्रतिवर्ती रॉयल जैकपॉट 1 के लिए 161,556 का भुगतान करता है। कोई भी अन्य रॉयल 1 के लिए 800 का भुगतान करता है। इस प्रकार औसत रॉयल जीत (1/60)*161,556 + (59/60)*800 + 17,396 1 के लिए है।

यदि हम यह मान लें कि सभी रॉयल्स 17,396 का भुगतान करते हैं और उस रॉयल जीत के आधार पर इष्टतम रणनीति अपनाते हैं, तो रिटर्न घटकर 103.56% हो जाता है।

यदि हम मानक 6-5 बोनस पोकर रणनीति, जो कि आधार भुगतान तालिका है, खेलते हैं, तो रिटर्न और भी कम होकर 101.97% हो जाता है।

निर्देशांक (0,0), (1,0), (1,1), (0,1) वाले इकाई वर्ग पर विचार करें। रेखा A, (0,0) से (1,1) तक जाती है। रेखा B, (1,0) से 0.5,1 तक जाती है। रेखाओं A, B और वृत्त के निचले भाग पर स्पर्श रेखा वाले वृत्त की त्रिज्या क्या है?

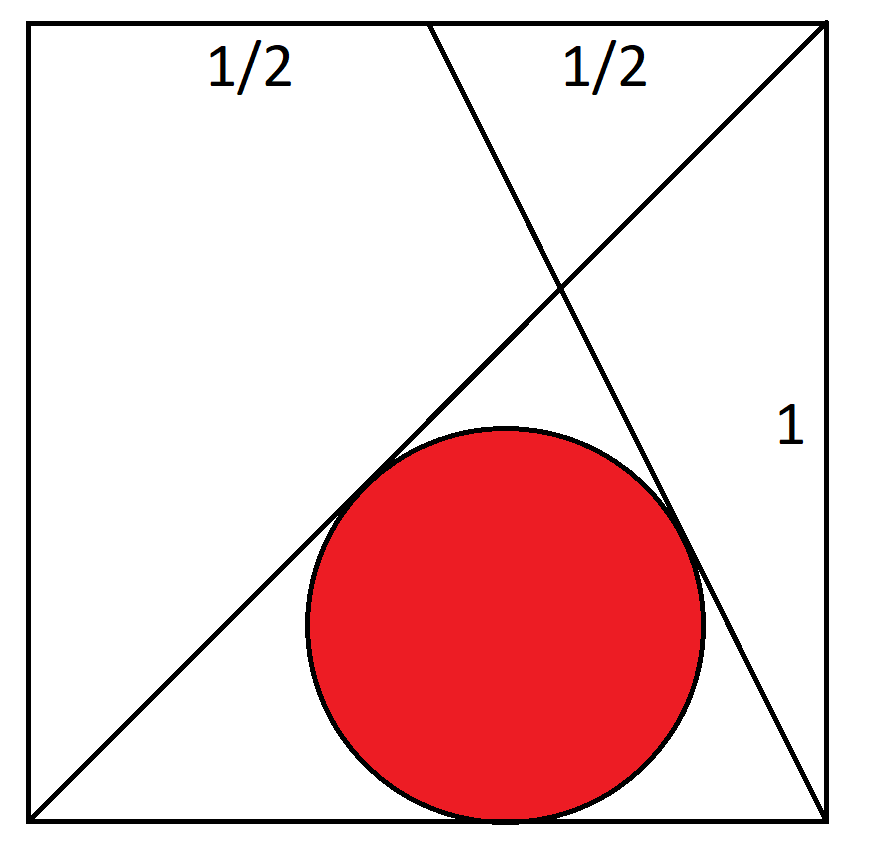
wizardofodds.com /wizfiles/img/2027/mensa-oct.png">

यह पहेली मेन्सा बुलेटिन के अक्टूबर 2020 संस्करण में छपी थी।

गुमनाम

[स्पॉइलर=संकेत]tan(2x)=2tan(x)/(1-tan 2 (x))[/स्पॉइलर]

उत्तर है (1+sqrt(2)+sqrt(5)-sqrt(10))/6 = लगभग 0.248000646617418.

यहां मेरा समाधान (पीडीएफ) है।

यह समस्या मेरे फोरम विजार्ड ऑफ वेगास में पूछी गई और इस पर चर्चा की गई।

यदि आपके कार्ड पर केवल यही श्रेणी बची है तो याहत्ज़ी मिलने की संभावना क्या है?

गुमनाम

याहत्ज़ी से अनभिज्ञ पाठकों के लिए, प्रश्न यह है कि पाँच पासों की तीन बार फेंके जाने पर एक ही तरह के पाँच आने की प्रायिकता क्या है। प्रत्येक बार फेंकने के बाद, आपको यह चुनना होगा कि कौन से पासे को अपने पास रखना है और कौन से पासे को दोबारा फेंकना है।

उत्तर 4.6029% है।

[स्पॉइलर=समाधान]

यहां पहले रोल या किसी भी रोल के बाद संभावित परिणाम दिए गए हैं जहां खिलाड़ी 4 या 5 पासे फेंकता है।

  • एक ही तरह के पाँच = 6*(1/6)^5 = 0.000772
  • एक तरह के चार = (1/6)^3*(5/6)*4 = 0.015432
  • एक तरह के तीन = (1/6)^2*(5/6)^2*COMBIN(4,2) = 0.115741
  • एक तरह के दो = 4*(1/6)*(5/6)^3 = 0.385802
  • एक तरह का = 6*5!/6^5 = 0.092593

यहां एक जोड़ी रखने के बाद संभावनाएं दी गई हैं।

  • एक ही तरह के पाँच =(1/6)^3 = 0.004630
  • एक तरह के चार = 3*(1/6)^2*(5/6) = 0.069444
  • एक तरह के तीन = 3*(1/6)*(5/6)^2+5*(1/6)^3 = 0.370370
  • एक तरह के दो = (5/6)^3-5*(1/6)^3 = 0.555555

एक तरह का तीन कार्ड मिलने के बाद संभावनाएं इस प्रकार हैं:

  • एक ही तरह के पाँच =(1/6)^3 = 0.002778
  • एक ही तरह के चार = 2*(1/6)*(5/6) = 0.27778
  • एक तरह के तीन = (5/6)^2 = 0.694444

एक तरह के चार कार्ड प्राप्त होने के बाद संभावनाएं इस प्रकार हैं:

  • एक तरह के पाँच =1/6 = 0.166667
  • एक ही तरह के चार = 5/6 = 0.83333

उन्नति की इन संभावनाओं के साथ, दूसरे रोल के बाद प्रत्येक राज्य की संभावनाएं इस प्रकार हैं:

  • एक तरह के पाँच = 0.000772 + 0.015432*0.166667 + 0.115741*0.002778 + 0.385802*0.004630 + 0.092593* 0.000772 = 0.012631
  • एक तरह के चार = 0.015432*0.166667 + 0.115741*0.27778 + 0.115741*0.27778 = 0.116970
  • एक तरह के तीन = 0.115741*0.694444 + 0.385802*0.370370 + 0.092593*0.115741 = 0.409022
  • एक ही तरह के दो = 0.385802*0.555555 + 0.092593*0.385802 = 0.450103
  • एक तरह का = 0.092593 * 0.092593 = 0.008573

उन्नति की समान संभावनाओं का उपयोग करते हुए, तीसरे रोल के बाद याहत्ज़ी की संभावना इस प्रकार है:

एक तरह के पांच = 0.012631 + 0.116970*(1/6) + 0.409022*(1/6)^2 + 0.450103*(1/6)^3 + 0.008573*(1/6)^4 = 0.046029.

आपमें से जो लोग मैट्रिक्स बीजगणित पसंद करते हैं, उनके लिए संक्रमण मैट्रिक्स है:

0.092593 0.694444 0.192901 0.019290 0.000772
0.000000 0.555556 0.370370 0.069444 0.004630
0.000000 0.000000 0.694444 0.277778 0.027778
0.000000 0.000000 0.000000 0.833333 0.166667
0.000000 0.000000 0.000000 0.000000 1.000000

यदि उपरोक्त मैट्रिक्स M है, तो तीन रोल के बाद स्थिति M 3 होगी, जो निम्नानुसार है:

0.000794 0.256011 0.452402 0.244765 0.046029
0.000000 0.171468 0.435814 0.316144 0.076575
0.000000 0.000000 0.334898 0.487611 0.177491
0.000000 0.000000 0.000000 0.578704 0.421296
0.000000 0.000000 0.000000 0.000000 1.000000

तीन रोल के बाद याहत्ज़ी होने की संभावना ऊपरी दाएं कोने में स्थित सेल में पाई जा सकती है।

[/बिगाड़ने वाला]

द क्वीन्स गैम्बिट देखने के बाद, मैंने देखा कि शो में कोई भी गेम ड्रॉ पर समाप्त नहीं हुआ। मुझे लगा कि उच्च स्तर पर शतरंज में बहुत सारे ड्रॉ होते हैं। ग्रैंडमास्टर स्तर के शतरंज में, कितने प्रतिशत गेम ड्रॉ पर समाप्त होते हैं?

गुमनाम

ChessBase.com पर प्रकाशित लेख "क्या शतरंज में ड्रॉ की संख्या बढ़ गई है?" के अनुसार, लेखक कियु झोउ ने बताया है कि 2600 या उससे अधिक (ग्रैंडमास्टर बनने के लिए 2500 अंक चाहिए) के खिलाड़ियों के बीच 78,468 रेटेड खेलों में, निम्नलिखित परिणाम सामने आए:

  • काला जीतता है: 18.0%
  • सफेद जीत: 28.9%
  • ड्रा: 53.1%