जादूगर से पूछो #326
क्रेप्स में आयरन क्रॉस रणनीति क्या है और आप इसके बारे में क्या सोचते हैं?
आयरन क्रॉस, 7 को छोड़कर, किसी भी पासे के रोल पर जीतने के लिए क्षेत्र और स्थान दांव लगाने का एक तरीका है। क्षेत्र में पहले से ही 2, 3, 4, 9, 10, 11 और 12 शामिल हैं। खिलाड़ी 7 के अलावा शेष संख्याओं को कवर करने के लिए 5, 6 और 8 पर स्थान दांव को जोड़ देगा। निम्नलिखित तालिका दिखाती है कि $5 क्षेत्र दांव, 5 पर $5 स्थान दांव, और 6 और 8 पर $6 स्थान दांव के साथ गणित कैसा दिखता है।
लोहे के पार
| पासा कुल | जीतना | युग्म | संभावना | वापस करना |
|---|---|---|---|---|
| 2 | 10 | 1 | 0.027778 | 0.277778 |
| 3 | 5 | 2 | 0.055556 | 0.277778 |
| 4 | 5 | 3 | 0.083333 | 0.416667 |
| 5 | 2 | 4 | 0.111111 | 0.222222 |
| 6 | 2 | 5 | 0.138889 | 0.277778 |
| 7 | -22 | 6 | 0.166667 | -3.666667 |
| 8 | 2 | 5 | 0.138889 | 0.277778 |
| 9 | 5 | 4 | 0.111111 | 0.555556 |
| 10 | 5 | 3 | 0.083333 | 0.416667 |
| 11 | 5 | 2 | 0.055556 | 0.277778 |
| 12 | 15 | 1 | 0.027778 | 0.416667 |
| 36 | 1.000000 | -0.250000 |
तालिका के निचले दाएँ भाग में $0.25 का अपेक्षित नुकसान दर्शाया गया है। कुल दांव राशि $22 है। इससे कुल हाउस एज $0.25/$22 = 1/88 = 1.14% हो जाता है।
इस बिंदु पर आप सोच रहे होंगे कि यह हाउस एज प्रत्येक व्यक्तिगत दांव के हाउस एज से कम कैसे हो सकता है। इसका उत्तर यह है कि 6 और 8 पर 1.52% और 5 पर 4.00% हाउस एज, प्रति दांव समाधान पर आधारित है। यदि हम प्रति रोल के आधार पर दांव लगाने पर हाउस एज निर्धारित करें, तो 6 या 8 पर हाउस एज 0.46% और 5 पर 1.11% है।
हम सभी दांवों का भारित औसत लेकर 1.14% हाउस एज प्राप्त कर सकते हैं, जो इस प्रकार है:
($5*2.78% + $5*1.11% + $12*0.46%)/22 = $0.25/$22 = 1.14%.
उन कैसिनो से सावधान रहें जो फ़ील्ड बेट पर 12 के लिए केवल 2 से 1 का भुगतान करते हैं। पूरे 3 से 1 पाने पर ज़ोर दें। शॉर्ट पे उस बेट पर हाउस एज को 2.78% से 5.56% तक दोगुना कर देता है।
मेरी राय में, ज़्यादातर खेलों की तुलना में, 1.14% एक काफ़ी अच्छा दांव है। हालाँकि, क्रेप्स में आप इससे भी बेहतर कर सकते हैं। उदाहरण के लिए, 3-4-5x ऑड्स के साथ, पास और कम पर दांव लगाने और पूरे ऑड्स के साथ, आप हाउस एज को 0.37% तक कम कर सकते हैं। इसके विपरीत, पास न होने और न आने पर दांव लगाने और पूरे ऑड्स लगाने पर, हाउस एज 0.27% हो जाता है।एक निष्पक्ष पासे के प्रत्येक फलक को कम से कम दो बार घुमाने के लिए अपेक्षित संख्या क्या है?
[स्पॉइलर=समाधान]
हालाँकि इसे एक लंबी और थकाऊ मार्कोव श्रृंखला से हल किया जा सकता है, मैं एक समग्र समाधान को प्राथमिकता देता हूँ। मैं फ़ायर बेट और बोनस क्रेप्स पर अपने पृष्ठों में इस विधि का उपयोग कैसे करें, यह समझाता हूँ।
कल्पना कीजिए कि महत्वपूर्ण घटनाओं को पासे के उछाल से, एक-एक करके, निर्धारित करने के बजाय, उन्हें समय के एक क्षण के रूप में मानिए। मान लीजिए कि घटनाओं के बीच का समय स्मृति-रहित है, यानी घटनाओं के बीच का औसत समय समय की एक इकाई है। दूसरे शब्दों में, घटनाओं के बीच का समय एक घातांकीय वितरण का अनुसरण करता है जिसका माध्य 1 है। बाजी तय करने के लिए यह मायने नहीं रखेगा, क्योंकि घटनाएँ फिर भी एक-एक करके घटित होती हैं।
पॉइसन वितरण के अनुसार, पासे के किसी भी दिए गए पक्ष को समय की x इकाई में शून्य बार घुमाए जाने की संभावना exp(-x/6)*(x/6) 0 /0! = exp(-x/6) है। पॉइसन का यह भी कहना है कि किसी भी पक्ष को ठीक एक बार घुमाए जाने की संभावना exp(-x/6)*(x/6) 1 /1! = exp(-x/6) * (x/6) है। इस प्रकार, किसी भी पक्ष को समय की x इकाई में दो या अधिक बार घुमाए जाने की संभावना 1 - exp(-x/6)*(1 + (x/6)) है। सभी छह पक्षों को कम से कम दो बार घुमाए जाने की संभावना (1 - exp(-x/6)*(1 + (x/6))) 6 है। कम से कम एक पक्ष को कम से कम दो बार घुमाए जाने की संभावना निम्न के बराबर है:
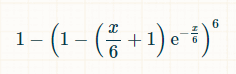
हमें इसे समग्र समय में एकीकृत करने की आवश्यकता है, ताकि पता चल सके कि औसतन कितना समय बीत जाएगा, जब वांछित लक्ष्य प्राप्त नहीं हुआ होगा।
सौभाग्य से, इस बिंदु पर हम एक समाकल कैलकुलेटर का उपयोग कर सकते हैं। लिंक किए गए कैलकुलेटर के लिए, "का समाकलन परिकलित करें" के बाद वाले टेक्स्ट बॉक्स में 1- (1 - exp(-x/6)*(1 + x/6))^6 dx = लगभग 24.1338692 लिखें और कस्टम के अंतर्गत, समाकलन की सीमा 0 से ∞ तक निर्धारित करें।
उत्तर है 390968681 / 16200000 = लगभग 24.13386919753086
[/spoiler]यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।
मेरा प्रश्न दो भागों में है।
भाग 1 के लिए, दिया गया:- x + y + z = 1
- x^2 + y^2 + z^2 = 4
- x^3 + y^3 + z^3 = 9
x^4 + y^4 + z^4 क्या है?
दूसरे भाग के लिए, सामान्य स्थिति का उत्तर क्या है जब:
- x + y + z = ए
- x^2 + y^2 + z^2 = बी
- x^3 + y^3 + z^3 = सी
प्रश्न 1: 97/6 = लगभग 16.166666
प्रश्न 2: a 4 /6 + (4/3)ac - a 2 b + b 2 /2
[स्पॉइलर=समाधान]
मेरा समाधान देखने के लिए (पीडीएफ)
[/spoiler]यह प्रश्न विज़ार्ड ऑफ़ वेगास में मेरे मंच पर उठाया गया है और इस पर चर्चा की गई है।
आप एक निष्पक्ष 6-पक्षीय पासे से शुरुआत करते हैं और उसे छह बार घुमाते हैं, और हर बार के परिणाम लिखते हैं। फिर आप इन संख्याओं को एक और बिना लेबल वाले निष्पक्ष पासे के छह फलकों पर लिखते हैं। उदाहरण के लिए, अगर आपके छह फलकों पर 3, 5, 3, 6, 1 और 2 आए, तो आपके दूसरे पासे पर 4 नहीं, बल्कि दो 3 होंगे।
इसके बाद, आप इस दूसरे पासे को छह बार घुमाते हैं। आप उन छह संख्याओं को एक और निष्पक्ष पासे के फलकों पर लिखते हैं, और पिछले पासे से एक नया पासा बनाने की प्रक्रिया जारी रखते हैं।
अंततः, आपके पास एक ऐसा पासा होगा जिसके सभी छह फलकों पर एक ही संख्या होगी। इस स्थिति तक पहुँचने के लिए एक पासे से दूसरे पासे में संक्रमणों की औसत संख्या (या कुल पासों को 6 से भाग देने पर) कितनी होगी?
[स्पॉइलर=समाधान]
भ्रम से बचने के लिए, आइए प्रारंभिक पासे को संख्याओं के बजाय अक्षरों से चिह्नित करें। आइए प्रत्येक संभावित पासे की स्थिति को अक्षरों से चिह्नित करें। उदाहरण के लिए, AAABBC का अर्थ होगा एक अक्षर के तीन, दूसरे के दो और तीसरे के एक। प्रारंभिक स्थिति स्पष्ट रूप से ABCDEF होगी।
मान लीजिए E(ABCDEF) राज्य ABCDEF से रोल की अपेक्षित संख्या है।
ई(एबीसीडीईएफ) = 1 + [180 × ई(एएएएएबी) + 450 × ई(एएएएबीबी) + 300 × ई(एएएबीबीबी) + 1800 × ई(एएएएबीसी) + 7200 × ई(एएएबीबीसी) + 1800 × ई(एएबीबीसीसी) + 7200 × ई(एएएबीसीडी) + 16200 × ई(एएबीबीसीडी) + 10800 × ई(एएबीसीडीई) + 720 × ई(एबीसीडीईएफ)]/46656एक अवस्था से दूसरी अवस्था में जाने के संयोजनों की संख्या के आधार पर, निम्नलिखित संक्रमण मैट्रिक्स दर्शाता है कि प्रत्येक प्रारंभिक अवस्था (बाएँ स्तंभ) से प्रत्येक नई अवस्था में जाने के कितने तरीके हैं। वैसे, इसे ठीक से बनाने में कुछ घंटे लगे।
संक्रमण मैट्रिक्स A
| राज्य पहले | आआआआ | आआआआब | आआआआब | एएएबीबीबी | एएएएबीसी | एएएबीबीसी | एएबीबीसीसी | एएएबीसीडी | एएबीबीसीडी | एएबीसीडीई | एबीसीडीईएफ |
|---|---|---|---|---|---|---|---|---|---|---|---|
| आआआआब | 15,626 | 18,780 | 9,750 | 2,500 | - | - | - | - | - | - | - |
| आआआआब | 4,160 | 13,056 | 19,200 | 10,240 | - | - | - | - | - | - | - |
| एएएबीबीबी | 1,458 | 8,748 | 21,870 | 14,580 | - | - | - | - | - | - | - |
| एएएएबीसी | 4,098 | 12,348 | 8,190 | 2,580 | 7,920 | 10,080 | 1,440 | - | - | - | - |
| एएएबीबीसी | 794 | 5,172 | 8,670 | 5,020 | 6,480 | 17,280 | 3,240 | - | - | - | - |
| एएबीबीसीसी | 192 | 2,304 | 5,760 | 3,840 | 5,760 | 23,040 | 5,760 | - | - | - | - |
| एएएबीसीडी | 732 | 4,464 | 4,140 | 1,680 | 7,920 | 14,400 | 2,520 | 4,320 | 6,480 | - | - |
| एएबीबीसीडी | 130 | 1,596 | 3,150 | 1,940 | 5,280 | 16,800 | 3,600 | 4,800 | 9,360 | - | - |
| एएबीसीडीई | 68 | 888 | 1,380 | 760 | 3,960 | 11,520 | 2,520 | 7,200 | 14,040 | 4,320 | - |
| एबीसीडीईएफ | 6 | 180 | 450 | 300 | 1,800 | 7,200 | 1,800 | 7,200 | 16,200 | 10,800 | 720 |
मैं मैट्रिक्स बीजगणित पर लंबा व्याख्यान नहीं दूंगा, सिवाय इसके कि मान लीजिए मैट्रिक्स B इस प्रकार है:
मैट्रिक्स बी
| राज्य पहले | आआआआब | आआआआब | एएएबीबीबी | एएएएबीसी | एएएबीबीसी | एएबीबीसीसी | एएएबीसीडी | एएबीबीसीडी | एएबीसीडीई | एबीसीडीईएफ |
|---|---|---|---|---|---|---|---|---|---|---|
| आआआआब | -27876 | 9750 | 2500 | 0 | 0 | 0 | 0 | 0 | 0 | -46656 |
| आआआआब | 13056 | -27456 | 10240 | 0 | 0 | 0 | 0 | 0 | 0 | -46656 |
| एएएबीबीबी | 8748 | 21870 | -32076 | 0 | 0 | 0 | 0 | 0 | 0 | -46656 |
| एएएएबीसी | 12348 | 8190 | 2580 | -38736 | 10080 | 1440 | 0 | 0 | 0 | -46656 |
| एएएबीबीसी | 5172 | 8670 | 5020 | 6480 | -29376 | 3240 | 0 | 0 | 0 | -46656 |
| एएबीबीसीसी | 2304 | 5760 | 3840 | 5760 | 23040 | -40896 | 0 | 0 | 0 | -46656 |
| एएएबीसीडी | 4464 | 4140 | 1680 | 7920 | 14400 | 2520 | -42336 | 6480 | 0 | -46656 |
| एएबीबीसीडी | 1596 | 3150 | 1940 | 5280 | 16800 | 3600 | 4800 | -37296 | 0 | -46656 |
| एएबीसीडीई | 888 | 1380 | 760 | 3960 | 11520 | 2520 | 7200 | 14040 | -42336 | -46656 |
| एबीसीडीईएफ | 180 | 450 | 300 | 1800 | 7200 | 1800 | 7200 | 16200 | 10800 | -46656 |
उत्तर मैट्रिक्स B का मैट्रिक्स A के निर्धारक के बराबर है:
निर्धारित करें(A) = 1,461,067,501,120,670,000,000,000,000,000,000,000,000,000,000
निर्धारित करें (B) = 14,108,055,348,203,100,000,000,000,000,000,000,000,000,000,000
निर्धारित करें(B) / निर्धारित करें(A) = लगभग 9.65599148388557
[/spoiler]

