जादूगर से पूछो #323
क्या यह पार्ले कार्ड अच्छा है?

पहले चरण में, आपको NFL गेम में स्प्रेड के विरुद्ध किसी भी तरफ दांव लगाना होगा। जब आपने यह प्रश्न पूछा था (2 जनवरी, 2020), उस समय वाइकिंग्स 7.5 अंकों से पिछड़ रहे थे। मेरे NFL वैकल्पिक पॉइंट स्प्रेड कैलकुलेटर के अनुसार, वाइकिंग्स +8.5 के उस तरफ जीतने की संभावना 52.22% है।
बाकी सभी खेलों के लिए, मैंने जीतने की संभावना जानने के लिए चल रही मनी लाइन्स को देखा, जूस को घटाया। इसके अलावा, नीचे दी गई तालिका प्रत्येक लेग की जीत की संभावना दर्शाती है।
विलियम हिल पार्ले कार्ड
| टांग | फेयर वाइन | संभवतः जीत |
|---|---|---|
| संत -8.5 | -7.5 | 47.78% |
| वाइकिंग्स +8.5 | 8.5 | 52.22% |
| होउ | -135 | 57.45% |
| विधेयकों | 135 | 42.55% |
| देशभक्त | -205 | 67.21% |
| टाइटन्स | 205 | 32.79% |
| समुद्र | -118 | 54.13% |
| फिल | 118 | 45.87% |
| एलएसयू | -200 | 66.67% |
| CLEMSON | 200 | 33.33% |
| एएफसी | -130 | 56.52% |
| एनएफसी | 130 | 43.48% |
चरण 1 में जीतने की सबसे ज़्यादा संभावना वाली दो टीमें पैट्रियट्स और एलएसयू हैं। मेरे सुझाए गए विकल्पों के जीतने की संभावना इस प्रकार है:
- वाइकिंग्स +8.5 — 52.22%
- देशभक्त — 67.21%
- एलएसयू — 66.67%
इन संभावनाओं का गुणनफल 23.40% है। 1 के बदले 4 प्राप्त करने पर 4 × 23.40% = 93.60% का रिटर्न मिलता है। दूसरे शब्दों में, हाउस एज 6.40% है। इसलिए, मैं इसे छोड़ दूँगा।
मैं "पुश 22" ब्लैकजैक वेरिएंट के लिए एक साइड बेट बनाने के बारे में सोच रहा हूं जो 11 से 1 का भुगतान करेगा यदि डीलर 22 के साथ बस्ट हो जाता है। ऑड्स क्या होंगे?
मैं "पुश 22" ब्लैकजैक वेरिएंट के लिए एक साइड बेट बनाने के बारे में सोच रहा हूं जो डीलर के 22 के साथ बस्ट होने पर जीत जाएगा। इसके लिए क्या ऑड्स का भुगतान करना चाहिए और हाउस एज क्या होगा?
यह मानते हुए कि डीलर हमेशा अपना हाथ निकालता है (भले ही हर खिलाड़ी पहले ही बस्ट हो चुका हो), तो मैं 22 पर बस्ट होने की संभावना 7.88% दिखाता हूं यदि डीलर सॉफ्ट 17 पर खड़ा है और 8.00% यदि वह सॉफ्ट 17 पर हिट करता है।
मान लीजिए कि डीलर सॉफ्ट 17 पर पहुँचता है, तो 11 से 1 की जीत पर हाउस एज 4.04% होगा। 10 से 1 पर, यह बढ़कर 12.04% हो जाता है।
मुझे आपको चेतावनी देनी चाहिए और खिलाड़ियों को सलाह देनी चाहिए कि यह गणना योग्य होगा (चुप रहो विज़!)।
एमी और बॉब के बीच एक निष्पक्ष सिक्के की चार उछालों में सबसे पहले जीतने की प्रतियोगिता है। एमी प्रतियोगिता जीतने के लिए खुद पर $8,000 का दांव लगाना चाहती है। हालाँकि, वह एक बार में केवल एक ही उछाल पर दांव लगा सकती है। सभी दांवों पर सम राशि मिलती है। वह अपने दांवों को इस तरह कैसे व्यवस्थित कर सकती है कि अगर वह पूरी श्रृंखला जीतती है तो $8,000 जीतती है और अगर बॉब जीतता है तो $8,000 हारती है?
उत्तर के लिए नीचे दिए गए बटन पर क्लिक करें।
श्रृंखला के मध्य में 16 संभावित स्थितियाँ हैं। नीचे दी गई तालिका दर्शाती है कि एमी को प्रत्येक पर कितना दांव लगाना चाहिए और इस रणनीति का पालन करते हुए दांव लगाने से पहले उसका शेष कितना है।
उत्तर
| एमी | बीओबी | संतुलन | शर्त |
|---|---|---|---|
| 0 | 0 | 0 | 2500 |
| 0 | 1 | -2500 | 2500 |
| 0 | 2 | -5000 | 2000 |
| 0 | 3 | -7000 | 1000 |
| 1 | 0 | 2500 | 2500 |
| 1 | 1 | 0 | 3000 |
| 1 | 2 | -3000 | 3000 |
| 1 | 3 | -6000 | 2000 |
| 2 | 0 | 5000 | 2000 |
| 2 | 1 | 3000 | 3000 |
| 2 | 2 | 0 | 4000 |
| 2 | 3 | -4000 | 4000 |
| 3 | 0 | 7000 | 1000 |
| 3 | 1 | 6000 | 2000 |
| 3 | 2 | 4000 | 4000 |
| 3 | 3 | 0 | 8000 |
समाधान के लिए नीचे दिए गए बटन पर क्लिक करें।
[स्पॉइलर=समाधान]होने देना:
- a = एमी जीतती है
- b = बॉब जीतता है
- w = एमी की अब तक श्रृंखला में कुल जीत
- f(a,b,w) = एमी का अगले गेम में दांव का आकार
इस तरह की पहेलियों में, शुरुआत और अंत से शुरुआत तक काम करना आम तौर पर एक अच्छी रणनीति होती है। हालाँकि, यह देखना आसान है कि:
f(3,3,0) = 8,000
इस स्थिति में, सातवाँ खेल "विजेता सब कुछ ले जाता है" वाला होता है। एमी को 0 की जीत हासिल करनी चाहिए और आखिरी फ़्लिप पर 8,000 का दांव लगाना चाहिए, जिससे अगर वह फ़्लिप जीतती है तो उसे 8,000 की जीत मिलेगी और अगर नहीं तो 8,000 की हार।
एक कदम पीछे चलते हैं, क्या होगा अगर उसे 3 जीतें और बॉब को 2। अगर वह अगला फ़्लिप जीत जाती है, तो वह पूरा खेल जीत जाती है। अगर वह हार जाती है, तो उसका स्कोर 3-3 होगा। f(3,3,0) से हम मानते हैं कि अगर स्कोर 3,3 है, तो उसे 0 मिलना चाहिए। इसलिए, अगर वह अगला फ़्लिप जीतती है, तो हमें उसके 8,000 चाहिए और नहीं तो 0। यहाँ 4,000 के बीच एक शुद्ध जीत और उतनी ही राशि का दांव मिलेगा। तो:
एफ(3,2,4000)=4,000
एक कदम और पीछे चलते हैं, क्या होगा अगर बॉब को 3 जीतें और बॉब को 1। अगर वह अगला फ़्लिप जीत जाती है, तो वह पूरा खेल जीत जाती है। अगर वह हार जाती है, तो उसका स्कोर 3-2 हो जाएगा। f(3,2,4000) से हम मानते हैं कि अगर स्कोर 3,2 है, तो उसके 4,000 होने चाहिए। इसलिए, अगर वह अगला फ़्लिप जीतती है, तो हमें उसके 8,000 और अगर नहीं, तो 4,000 चाहिए। यहाँ जो मिलेगा वह बीच में एक शुद्ध जीत होगी [(4,000+8,000)/2=6,000] और उन दो गोलों के बीच की आधी दूरी का दांव, [(8000-4000)/2 = 2000]। तो:
f(3,1,6000) = 2,000
एक कदम और पीछे चलते हैं, क्या होगा अगर बॉब को 3 जीतें और बॉब को 0। अगर वह अगला फ़्लिप जीत जाती है, तो वह पूरा खेल जीत जाती है। अगर वह हार जाती है, तो उसका स्कोर 3-1 हो जाएगा। f(3,1,6000) से हम मानते हैं कि अगर स्कोर 3,1 है, तो उसके 6,000 होने चाहिए। इसलिए, अगर वह अगला फ़्लिप जीतती है, तो हमें उसके 8,000 और अगर नहीं, तो 6,000 चाहिए। यहाँ जो मिलेगा वह बीच में एक शुद्ध जीत होगी [(6,000+8,000)/2=7,000] और उन दो गोलों के बीच की आधी दूरी का दांव, [(8000-4000)/2 = 2000]। तो:
f(3,0,7000) = 1,000
उम्मीद है कि अगर स्कोर कभी बराबर हो जाए तो एमी की कुल जीत 0 होनी चाहिए। किसी भी बराबरी की स्थिति में, पूरी सीरीज़ जीतने की उसकी संभावना 50% होगी। 8,000 के जीत/हार के संतुलित लक्ष्यों के साथ, उसे 0 पर दांव लगाना होगा, अन्यथा उसके किसी भी अंतिम लक्ष्य को हासिल न करने की संभावना होगी।
इसके बाद, अगर एमी कभी भी सीरीज़ में पीछे रहती है, तो उसकी नेट जीत, उसी स्कोर से आगे होने पर नेट जीत की -1 गुना होनी चाहिए। उदाहरण के लिए, एमी का स्कोर 2 - बॉब 3 (या 2-3) मान लीजिए। अगर वह अगला फ़्लिप हार जाती है, तो वह पूरा खेल हार जाती है। अगर वह जीत जाती है, तो उसका स्कोर 3-3 हो जाएगा। f(3,3,0) से हम मानते हैं कि अगर स्कोर 3,3 है, तो उसे 0 मिलना चाहिए। इसलिए, अगर वह अगला फ़्लिप जीतती है, तो हमें 0 मिलना चाहिए और अगर नहीं, तो -8000। यहाँ 4,000 के बीच का नेट घाटा और उतनी ही राशि का दांव होगा। तो:
एफ(2,3,-4000)=4,000
इसी तर्क से:
f(1,3,-6000) = 2,000
f(0,3,-7000) = 1,000
अब, अगर स्कोर 2-2 है, तो एमी को क्या दांव लगाना चाहिए? अगर वह फ्लिप जीत जाती है, तो स्कोर 3-2 होगा। ऊपर दिए गए आंकड़े से, हम देख सकते हैं कि इस स्कोर के साथ उसे 4,000 की शुद्ध जीत हासिल करनी होगी। हम यह भी देख सकते हैं कि अगर वह 2-3 से पिछड़ रही है, तो हमें उसे 4,000 का शुद्ध नुकसान उठाना होगा। इसलिए, उसे 4,000 का दांव लगाना होगा:
f(2,2,0) = 4,000
वहाँ से एक कदम पीछे चलते हैं, अगर स्कोर 2-1 हो तो क्या होगा? हमने तय किया है कि अगर वह अगला फ़्लिप जीतती है (स्कोर 3-1) तो उसे 6,000 की नेट जीत चाहिए और अगर वह हारती है (स्कोर 2-2)। यहाँ जो मिलेगा वह बीच में नेट जीत होगी [(6,000+0)/2=3,000] और उन दो गोलों के बीच की आधी दूरी का दांव, [(6,000-0)/2=3,000]। तो:
एफ(2,1,3000) = 3000
वहाँ से एक कदम पीछे चलते हुए, क्या होगा अगर बॉब को 2 जीतें और बॉब को 0। अगर वह अगला फ़्लिप जीतती है, तो स्कोर 3-0 होगा। अगर वह हारती है, तो स्कोर 2-1 होगा। 3-0 पर उसकी कुल जीत 7000 और 2-1 पर 3000 होनी चाहिए। 2-0 के स्कोर से यहाँ-वहाँ क्या होगा, बीच में एक कुल जीत [(7,000+3,000)/2=5,000] और उन दो गोलों के बीच की आधी दूरी का दांव, [(7000-3000)/2=2,000]। तो:
एफ(2,0,5000) = 2000
उन अंकों को पलटने पर, जहां ऐलिस की दो जीतें हैं और बॉब की कम, हम यह भी जानते हैं:
एफ(1,2,-3000) = 3000
एफ(0,2,-5000) = 2000
जैसा कि पहले बताया गया है, अगर सीरीज़ बराबर है, तो एमी की नेट जीत 0 होनी चाहिए, इसलिए 1-1 के स्कोर पर उसकी नेट जीत 0 होनी चाहिए। 2-1 के स्कोर पर उसे 2,000 से आगे और 1-2 के स्कोर पर 2,000 से पीछे होना होगा। इसलिए, 1-1 के बराबर स्कोर पर उसे 2,000 का दांव लगाना चाहिए, या:
f(1,1,0) = 2,000
अगर एमी 1-0 से आगे हो जाए तो क्या होगा? हमने तय किया है कि 2.0 पर उसे 5,000 से आगे होना होगा। 1-1 पर उसे बराबरी पर होना होगा।1-0 के स्कोर से यहाँ-वहाँ जो होगा वह बीच में एक शुद्ध जीत होगी [(5,000+0)/2=2,500] और उन दो गोलों के बीच की आधी दूरी का दांव, [(5000-0)/2=2,500]। तो:
एफ(1,0,2500) = 2,500
स्कोर को 0-1 पर लाकर:
f(0,1,-2500) = 2,500
तो, आखिरकार, हम पहले गेम में 0-0 के स्कोर पर हैं। हमें एमी को अगला फ़्लिप जीतने पर 2,500 का फायदा और हारने पर 2,500 का नुकसान चाहिए। इस तरह, 2,500 का दांव हमें वहाँ पहुँचा देगा। या:
एफ(0,0,0) = 2,500
[/spoiler]यह प्रश्न विज़ार्ड ऑफ़ वेगास में मेरे मंच पर उठाया गया है और इस पर चर्चा की गई है।
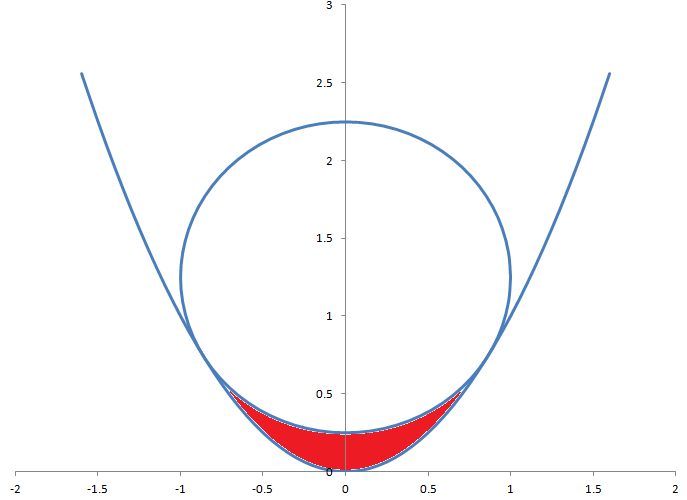
त्रिज्या 1 वाला एक वृत्त समीकरण y=x 2 वाले परवलय पर स्पर्शरेखा है। वृत्त और परवलय के बीच लाल रंग के क्षेत्र का क्षेत्रफल क्या है?
उत्तर के लिए नीचे दिए गए बटन पर क्लिक करें।
मेरा समाधान यहां है (पीडीएफ)
यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।
मुझे यह समस्या माइंड योर डिसीजन्स के प्रेश तलवाल्कर से मिली।


