जादूगर से पूछो #322
मैं टेक्सास होल्ड 'एम खेल रहा था और चल रहे हाथ के दौरान सबसे बड़ा हाथ स्ट्रेट फ्लश था। टेबल पर बैठे दो अन्य खिलाड़ियों ने कहा कि यह लगातार तीसरा स्ट्रेट फ्लश था। इसकी संभावना क्या है?
टेक्सास होल्ड 'एम के दस खिलाड़ियों वाले खेल में, यह मानते हुए कि कोई भी कभी फ़ोल्ड नहीं करता, हाई हैंड के स्ट्रेट या रॉयल फ्लश होने की संभावना 350.14 में 1 है। तीन में से तीन हैंड में ऐसा होने की संभावना 42,926,491 में 1 है।
हालाँकि, हो सकता है कि वह टेबल घंटों से चल रही हो। शायद ज़्यादा व्यावहारिक सवाल यह है कि पूरे दिन में कम से कम एक बार ऐसा होने की क्या संभावना है। पूरे 24 घंटे का खेल और प्रति घंटे 24 हाथ मानकर, इस सवाल का जवाब 59,621 में से 1 होगा।
यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।
सही रणनीति मानते हुए, अल्टीमेट टेक्सास होल्ड 'एम में 4x रेज मिलने पर जीतने की संभावना क्या है? मैंने 96 4x हैंड दर्ज किए। पुश को छोड़कर, मुझे 66 जीत और 30 हार मिलीं। यह उम्मीदों से कितना मेल खाता है?
सही 4x बढ़ाने की रणनीति मानते हुए, 4x बढ़ाने पर प्रत्येक परिणाम की संभावना इस प्रकार है:
- जीत: 58.82%
- हानि: 38.47%
- टाई: 2.72%
अगर हम बराबरी वाले ड्रा को हटा दें, तो जीतने की संभावना 60.46% है। 96 बार हल किए गए ड्रा में, 4x जीत की अपेक्षित संख्या 58.04 है। इसलिए, 66 जीत उम्मीद से ज़्यादा है, लेकिन बहुत ज़्यादा नहीं।
यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।
एक्सल और बॉब, दोनों के पास 52 पत्तों का अपना डेक है। दोनों उन्हें बेतरतीब ढंग से फेंटते हैं। फिर वे हर डेक से एक-एक पत्ता एक साथ पलटते हैं। क्या संभावना है कि वे एक ही समय पर कम से कम एक बार एक ही पत्ता पलटें?
उत्तर का अनुमान लगाना आसान होगा: 1-(51/52) 52 = 0.63568648। हालाँकि, ये अनुमान बौद्धिक रूप से बहुत असंतोषजनक हैं। तो, आइए एक सटीक समाधान खोजें!
चरण 1: शुरू करने के लिए, दूसरे डेक को ऑर्डर करने के तरीकों की संख्या पर विचार करें जहां पहला कार्ड नंबर 1 है। उत्तर अन्य 51 कार्डों को ऑर्डर करने के तरीकों की संख्या है, जो 51 है! = 1551118753287382280224243016469303211063259720016986112000000000000.
कोई भी पत्ता पहले डेक से मेल खा सकता है, इसलिए हमें सभी 52 पत्तों के लिए ऐसा करना होगा। इससे हमें 52*51! = 52! संयोजन मिलते हैं जहाँ कम से कम एक पत्ता मेल खाता है।
चरण 2: हालांकि, चरण 1 हर उस स्थिति को दोगुना गिनता है जहां दो कार्ड मेल खाते हैं। उदाहरण के लिए, यदि पहले दो कार्ड 1 और 2 थे, तो हम अन्य कार्डों को व्यवस्थित करने के 50! तरीकों को दो बार गिनते, एक बार 1 को पहला कार्ड और दूसरी बार 2 को दूसरा कार्ड मानते हुए। 52 में से 2 कार्ड चुनने के तरीकों की संख्या combin(52,2) = 1326 है। दो कार्डों के प्रत्येक संयोजन के लिए, अन्य कार्डों को क्रम से लगाने के 50! = 304140932017133780436126081660647688443776415689605120000000000000
चरण 3: इसके बाद, उस स्थिति पर विचार करें जहां यादृच्छिक डेक में पहले तीन कार्ड क्रमशः 1, 2 और 3 हैं। अन्य 49 कार्डों को क्रमबद्ध करने के 49! तरीके हैं। कम से कम एक मिलान वाले कार्ड की गिनती के प्रारंभिक चरण में हमने उन्हें तीन बार गिना होगा। फिर हमने दूसरे चरण में इन तीन कार्डों में से 2 को चुनने के लिए सभी combin(3,2)=3 तरीकों को घटा दिया होगा। तो यह स्थिति 3-3=0 बार गिनी गई होगी, इसलिए हमें उन्हें वापस जोड़ना होगा। कम से कम 3 कार्ड चुनने के combin(52,3) ऐसे हालात हैं जो मेल खाते हैं। इसलिए हमें combin(52,3)*49! = 52*51*50*49!/3! = 52!/3! संयोजनों को वापस जोड़ना होगा।
चरण 4: इसके बाद, उस स्थिति पर विचार करें जहां यादृच्छिक डेक में पहले चार कार्ड क्रमशः 1, 2, 3 और 4 हैं। अन्य 48 कार्डों को क्रमबद्ध करने के 48! तरीके हैं। कम से कम एक मिलान कार्ड की गिनती के प्रारंभिक चरण में हमने उन्हें चार बार गिना होगा। फिर हमने चरण 2 में इन चार कार्डों में से दो को चुनने के लिए सभी combin(4,2)=6 तरीकों को घटाया होगा। फिर हमने इन चार कार्डों में से 3 को चुनने के लिए सभी combin(4,3)=4 तरीकों को जोड़ा होगा। तो हम 4-6+4=2 तरीकों पर हैं, प्रत्येक ऐसी स्थिति को गिना गया होगा। इसलिए हमें उन तरीकों में से एक को घटाने की जरूरत है, ताकि प्रत्येक स्थिति को एक बार गिना जाए। ऐसी कई स्थितियाँ हैं combin(52,4)*48! = 52*51*50*49*48!/4! = 52!/4!
हम ऐसा करते रहेंगे, दोहरी गिनती को ठीक करने के लिए बारी-बारी से जोड़ और घटाव करेंगे।
अंत में, उन स्थितियों की संख्या जहां यादृच्छिक डेक में कम से कम एक कार्ड क्रमबद्ध डेक से मेल खाता है = combin(52,1)*51! - combin(52,2)*50! + combin(52,3)*49! - combin(52,4)*48! ... - combin(52,52)*1! = 52!/1! - 52!/2! + 52!/3! - 52!/4! ... - 52!/52! = x = 333239808909468890675694068318655265019682314241643033726180828783.
52 कार्ड ऑर्डर करने के कुल तरीके 52 हैं! = y = 52717761549636521942261854154512265996921245386198220800000000000000 हैं।
इस प्रकार, उत्तर है x/y = 0.6321205588285576784044762298
कोई मिलान न होने की संभावना 1-(x/y) = 0.3678794411714423215955237702 है।
यदि यह संख्या परिचित लगती है, तो ऐसा होना चाहिए। 1/e = 0.3678794411714423215955237702.
अतः, उत्तर का अनुमान बहुत ही बारीकी से 1-(1/e) के रूप में लगाया जा सकता है।
स्वीकृतियाँ
गणितीय गणना Pari/GP में की गई
यह समस्या मेरे फोरम विजार्ड ऑफ वेगास में पूछी गई और इस पर चर्चा की गई।
आपकी साइट पर बिंगो पैटर्न प्रोबेबिलिटीज़ (पीडीएफ) नामक दस्तावेज़ में, आप विजेता को खोजने के लिए अपेक्षित कॉल की संख्या इंगित करते हैं, यह मानते हुए कि खेल में 300 कार्ड हैं, जो इस प्रकार है:
- चार कोने: 8.43
- छोटा हीरा: 11.833
दोनों पैटर्न में केवल चार अंक चाहिए और जीतने का केवल एक ही तरीका है। विजेता चुनने के लिए गेंदों की अपेक्षित संख्या अलग-अलग क्यों है?
इसका उत्तर समझाना मुश्किल है। मैं यह कहकर शुरुआत करूँगा कि एक-पत्तों वाले खेल में अपेक्षित कॉलों की संख्या समान होगी। हालाँकि, एक से ज़्यादा पत्तों के साथ एक सहसंबंध प्रभाव होता है।
इसका तुरंत जवाब देना मुश्किल है, लेकिन अगर ज़ोर दिया जाए, तो ऐसा इसलिए है क्योंकि चार कोनों वाले पैटर्न में B और O स्तंभों में गेंदों का जमावड़ा ज़रूरी होता है। छोटे हीरे वाले पैटर्न में B, N और O स्तंभों पर गेंदों का समतल वितरण होने पर हिट होने की संभावना ज़्यादा होती है।
आइए इस खेल को सरल बनाते हैं, जहाँ अनंत संख्या में कार्ड होते हैं और गेंदें प्रतिस्थापन के साथ निकाली जाती हैं। दोनों खेलों में विजेता बनने के लिए आवश्यक गेंदों की संख्या इस प्रकार है:
- चार कोने: 2.5+2.5+((1/2)*10+(1/2)*(2.5+5)) = 13.75
- छोटा हीरा: =(5/3)+((1/3)*((5/3)+(5/2)+5)+(2/3)*((5/2)+((1/2)*((5/2)+5)+(1/2)*(5+5)))) = 12 + 2/9
इससे पता चलता है कि चारों कोनों तक पहुंचने में 1.53 गेंदें अधिक लगेंगी।
सामान्य बिंगो नियमों के तहत इसे एक साथ चलाने पर, अनंत कार्ड मानते हुए, परिणाम इस प्रकार हैं:
- चार कोने: 12.8289
- हीरा: 11.3645
इस बार 1.46 गेंदों का अंतर है।
मुझे उम्मीद है कि मैंने यह दिखा दिया होगा कि अगर अंक ज़्यादा कॉलम में बाँटे जाएँ, तो पैटर्न जल्दी समझ में आ जाते हैं। इसी वजह से, मुझे लगता है कि सिंगल-बिंगो गेम में आप आमतौर पर देखते हैं कि जीतने वाला बिंगो क्षैतिज होता है।
यह प्रश्न विज़ार्ड ऑफ़ वेगास में मेरे मंच पर चर्चा में पूछा गया है।
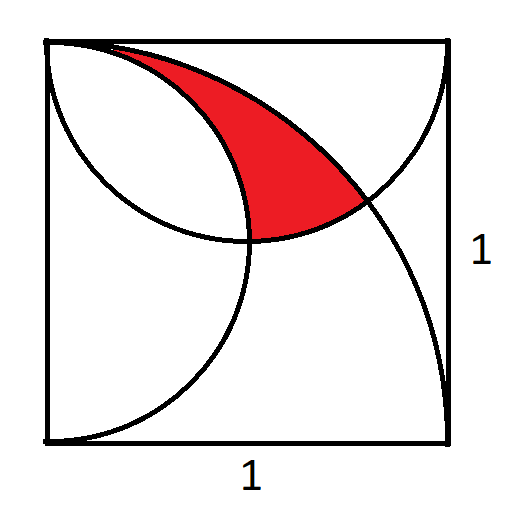
ऊपर दी गई आकृति में, एक भुजा वाले वर्ग में एक चौथाई वृत्त और दो अर्धवृत्त हैं। प्रश्न यह है कि लाल क्षेत्र का क्षेत्रफल क्या है?
मेरे उत्तर के लिए निम्नलिखित बटन पर क्लिक करें।
मेरे समाधान के लिए निम्नलिखित बटन पर क्लिक करें।
[स्पॉइलर=समाधान]यहाँ मेरे समाधान का लिंक है। (पीडीएफ)[/spoiler]
यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।
आभार: मैं इस गणित पहेली के लिए माइंड योर डिसीजन्स को धन्यवाद देना चाहता हूँ।


