जादूगर से पूछो #321
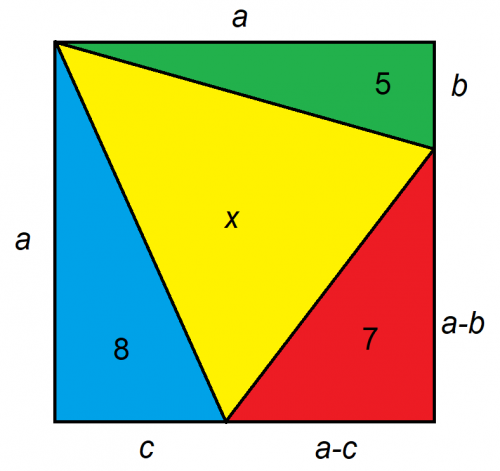
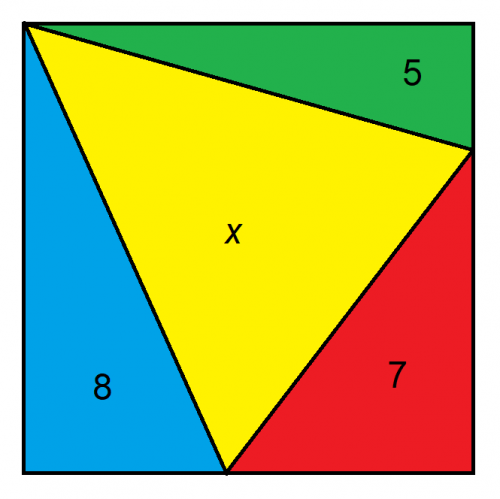
दिया गया है कि बड़ी आकृति एक वर्ग है, x का क्षेत्रफल क्या है?
इस तरह की समस्याओं की कुंजी उन्हें व्यवस्थित करने में है। मेरा सुझाव है कि समस्या को यथासंभव कम अज्ञात मानों तक सीमित रखने का प्रयास करें। इस स्थिति में, हम वर्ग पर अज्ञात दूरियों को केवल तीन में व्यक्त कर सकते हैं, इस प्रकार:
त्रिभुजों की तुलना में आयतों से निपटना आसान होता है। चूँकि हमें तीन त्रिभुजों का क्षेत्रफल पता है, इसलिए हम उनका आकार और क्षेत्रफल दोगुना कर सकते हैं। इससे हमें मिलता है:
- अब=10
- एसी=16
- (एबी)(एसी)=14
आइए (ab)(ac) का गुणनखंड करें:
a 2 - ab- ac + bc = 14
a 2 - 10 - 16 + bc = 14
(1) a 2 + bc = 40
आइए b और c को a के रूप में व्यक्त करें, ताकि इसे एकल चर में लाया जा सके:
बी = 10/ए
सी = 16/ए
समीकरण (1) में b और c के लिए उन मानों को प्रतिस्थापित करने पर:
ए 2 + (10/ए)*(16/ए) = 40
a 2 + 160/a 2 = 18
अब, आइए सभी चीजों को 2 से गुणा करके हर में से 2 को हटा दें।
ए 4 + 160 = 40*ए 2
ए 4 - 40*ए 2 + 160 = 0
आइए एक नया चर y = a 2 परिभाषित करें
y 2 - 18y + 32 = 0
अब, आइए द्विघात सूत्र का उपयोग करके y का हल निकालें:
y = (40 +/- sqrt(1600-640))/2
y = (40 +/- sqrt(960))/2
y = (40 +/- 8*sqrt(15))/2
y = 20 +/- 4*sqrt(15)
पूरे वर्ग का क्षेत्रफल a 2 है, जो सुविधाजनक रूप से y के बराबर है। उपरोक्त समीकरण से, यदि +/- ऋणात्मक है, तो y = लगभग 4.5081 है, जो स्पष्ट रूप से गलत है, क्योंकि हम जानते हैं कि क्षेत्रफल कम से कम 20 है, जिसमें x भी शामिल नहीं है। इसलिए वर्ग का क्षेत्रफल 20 + 4*sqrt(15) होना चाहिए।
हमें दिए गए तीन त्रिभुजों का क्षेत्रफल 5+7+8=20 है। इसे वर्ग के कुल क्षेत्रफल से घटाने पर हमें x का क्षेत्रफल प्राप्त होता है: 20 + 4*sqrt(15) - 20 = 4*sqrt(15) = लगभग 15.4919।
यह प्रश्न विज़ार्ड ऑफ़ वेगास में मेरे मंच पर उठाया गया है और इस पर चर्चा की गई है।

इस तस्वीर में मेरी टी-शर्ट देखिये। जब मैं "अनकट जेम्स" देखने गया था, तो सिनेमाघर के कैशियर ने इसकी तारीफ़ की थी। मैंने उसे इस समस्या से परेशान करके धन्यवाद दिया, सिर्फ़ क्षेत्रफल 2, 3 और 4 के त्रिभुजों से। फिल्म के बाद, मैंने उससे पूछा कि उसने अभी तक इसे हल नहीं किया था, लेकिन ऐसा लग रहा था कि वह कोशिश कर रही है। इसलिए मैंने सनकोस्ट बार में उसके लिए यह हल लिखा। उसे वाकई यह पसंद आया। मुझे लगता है कि वह युवती ज़िंदगी में बहुत आगे जाएगी।
लॉटरी के संदर्भ में, क्या बहु-राज्य लॉटरी (पॉवरबॉल, मेगा मिलियंस) में जैकपॉट के आकार का कोई "टिपिंग पॉइंट" होता है, जहाँ बड़े पुरस्कार के बँट जाने की संभावना ज़्यादा होती है, बजाय इसके कि एक विजेता हो? यदि हाँ, तो वह राशि कितनी होती है?
मैं सभी गणित में नहीं जाऊंगा, लेकिन यहां जैकपॉट बिंदु हैं जहां एक से अधिक विजेताओं की संभावना एक के बराबर है:
- पावरबॉल: $975 मिलियन
- मेगा मिलियन्स: 1.65 बिलियन डॉलर
ऐसा नहीं है कि आपने पूछा था, लेकिन यहां कुछ जैकपॉट हैं जहां कम से कम एक विजेता की संभावना किसी के न जीतने की संभावना (50%) के बराबर है।
- पावरबॉल: 704 मिलियन डॉलर
- मेगा मिलियन्स: $867 मिलियन
यह प्रश्न विज़ार्ड ऑफ वेगास में मेरे मंच पर चर्चा में उठाया गया है।
- एक जेल में 12 कैदी हैं, जिनमें से प्रत्येक की संख्या 1 से 12 तक है।
- वार्डन 12 बक्से लगाता है, जिनमें से प्रत्येक पर 1 से 12 तक संख्या अंकित होती है।
- 12 बक्सों के अंदर 1 से 12 तक की संख्याएं यादृच्छिक रूप से रखी गई हैं, प्रत्येक बक्से में एक।
- प्रत्येक कैदी को एक-एक करके अपनी पसंद के छह बक्से खोलने की अनुमति होगी। वह एक-एक करके उन्हें चुनकर खोल सकता है।
- हर कैदी का लक्ष्य एक डिब्बे के अंदर, अपने छह विकल्पों में से अपना नंबर ढूँढ़ना होता है। अगर वह ऐसा कर लेता है, तो माना जाता है कि वह बच गया है।
- यदि किसी कैदी को अपना नंबर नहीं मिलता है, तो पूरे समूह को असफल माना जाता है और उन्हें तुरंत फायरिंग दस्ते के पास ले जाया जाता है।
- यदि कोई कैदी बच जाता है, तो उसे अगले कैदी के लिए संख्याओं को उनके मूल बक्सों में वापस रखना होगा।
- खेल शुरू होने के बाद कैदी अन्य खिलाड़ियों को नहीं देख सकते हैं या उनसे बातचीत नहीं कर सकते हैं।
- शुरुआत से पहले, पूरे समूह को एक रणनीति पर मिलकर काम करने की अनुमति दी जाती है। लक्ष्य यह है कि सभी 12 कैदी बच जाएँ (दूसरे शब्दों में, एक डिब्बे के अंदर अपना नंबर ढूँढ़ें)।
जीवित रहने की संभावना को अधिकतम करने के लिए उनकी रणनीति क्या होनी चाहिए और वह संभावना क्या है?
[स्पॉइलर=समाधान]
सीक्रेट सांता गेम की तरह, इसमें भी एक नंबर से दूसरे नंबर तक जाने वाले लूप होंगे। 12 कैदियों के साथ, 1 से 12 लूप हो सकते हैं। अगर कोई भी लूप छह से ज़्यादा लंबा नहीं है, तो हर कैदी आखिरकार अपना नंबर ढूंढ ही लेगा। बड़ा सवाल यह है कि छह से बड़ा कोई लूप न होने की प्रायिकता क्या है? आइए इसे उलट दें और 7 या उससे ज़्यादा आकार वाले लूप के संयोजनों की संख्या ज्ञात करें।
12 कैदी समाधान
| छोरों | युग्म | संभावना |
|---|---|---|
| 12 | 39,916,800 | 0.083333 |
| 11,1 | 43,545,600 | 0.090909 |
| 10,2 | 23,950,080 | 0.050000 |
| 10,1,1 | 23,950,080 | 0.050000 |
| 9,3 | 17,740,800 | 0.037037 |
| 9,2,1 | 26,611,200 | 0.055556 |
| 9,1,1,1 | 8,870,400 | 0.018519 |
| 8,4 | 14,968,800 | 0.031250 |
| 8,3,1 | 19,958,400 | 0.041667 |
| 8,2,2 | 7,484,400 | 0.015625 |
| 8,2,1,1 | 14,968,800 | 0.031250 |
| 8,1,1,1,1 | 2,494,800 | 0.005208 |
| 7,5 | 13,685,760 | 0.028571 |
| 7,4,1 | 17,107,200 | 0.035714 |
| 7,3,2 | 11,404,800 | 0.023810 |
| 7,3,1,1 | 11,404,800 | 0.023810 |
| 7,2,2,1 | 8,553,600 | 0.017857 |
| 7,2,1,1,1 | 5,702,400 | 0.011905 |
| 7,1,1,1,1,1 | 570,240 | 0.001190 |
| कुल | 312,888,960 | 0.653211 |
निम्नलिखित तालिका उपरोक्त तालिका में दिए गए संयोजनों के सूत्र दर्शाती है।
संयोजन सूत्र
| छोरों | युग्म | FORMULA |
|---|---|---|
| 12 | 39916800 | =तथ्य(11) |
| 11,1 | 43545600 | =कॉम्बिन(12,11)*फैक्ट(10) |
| 10,2 | 23950080 | =कॉम्बिन(12,10)*फैक्ट(9) |
| 10,1,1 | 23950080 | =कॉम्बिन(12,10)*फैक्ट(9) |
| 9,3 | 17740800 | =कॉम्बिन(12,9)*तथ्य(8)*तथ्य(2) |
| 9,2,1 | 26611200 | =कॉम्बिन(12,9)*कॉम्बिन(3,2)*तथ्य(8) |
| 9,1,1,1 | 8870400 | =कॉम्बिन(12,9)*फैक्ट(8) |
| 8,4 | 14968800 | =कॉम्बिन(12,8)*तथ्य(7)*तथ्य(3) |
| 8,3,1 | 19958400 | =कॉम्बिन(12,8)*कॉम्बिन(4,3)*तथ्य(7)*तथ्य(2) |
| 8,2,2 | 7484400 | =कॉम्बिन(12,8)*कॉम्बिन(4,2)*तथ्य(7)/2 |
| 8,2,1,1 | 14968800 | =कॉम्बिन(12,8)*कॉम्बिन(4,2)*तथ्य(7) |
| 8,1,1,1,1 | 2494800 | =कॉम्बिन(12,8)*फैक्ट(7) |
| 7,5 | 13685760 | =कॉम्बिन(12,7)*तथ्य(6)*तथ्य(4) |
| 7,4,1 | 17107200 | =कॉम्बिन(12,7)*5*तथ्य(6)*तथ्य(3) |
| 7,3,2 | 11404800 | =कॉम्बिन(12,7)*कॉम्बिन(5,3)*तथ्य(6)*तथ्य(2) |
| 7,3,1,1 | 11404800 | =कॉम्बिन(12,7)*कॉम्बिन(5,3)*तथ्य(6)*तथ्य(2) |
| 7,2,2,1 | 8553600 | =कॉम्बिन(12,7)*कॉम्बिन(5,2)*कॉम्बिन(3,2)*तथ्य(6)/2 |
| 7,2,1,1,1 | 5702400 | =कॉम्बिन(12,7)*कॉम्बिन(5,2)*तथ्य(6) |
| 7,1,1,1,1,1 | 570240 | =कॉम्बिन(12,7)*फैक्ट(6) |
पहली तालिका के निचले दाएँ कक्ष में, 312,888,960 असफल संयोजन हैं। संख्याओं को व्यवस्थित करने के कुल तरीकों की संख्या 12! = 479,001,600 है। इस प्रकार, असफलता की संभावना 312,888,960 / 479,001,600 = 65.32% है। इसलिए, सफलता की संभावना 100% - 65.32% = 34.68% है।
[/spoiler]यह प्रश्न विज़ार्ड ऑफ़ वेगास में मेरे मंच पर उठाया गया है और इस पर चर्चा की गई है।
नमस्ते। मेरे पास एक कूपन है जिससे मैं 22 का हाथ पुश कर सकता हूँ। मैं इस कूपन को अपने पहले 22 तक रख सकता हूँ। यह डबल्स या स्प्लिट्स पर लागू नहीं होता। इसका मूल्य क्या है?
एक त्वरित उत्तर यह है कि आप अधिकतम कितना दांव लगा सकते हैं। बस 22 का इंतज़ार करें और फिर दांव लगाएँ, जिससे आप एक अतिरिक्त यूनिट लेकर टेबल से बाहर निकल जाएँगे।
एक अधिक कठोर उत्तर में उस 22 के लिए प्रतीक्षा करने की लागत पर विचार किया जाना चाहिए। यह ऐसी बात है जिसके बारे में मुझे ठीक-ठीक जानकारी नहीं है, लेकिन मैं इसका अनुमान लगा सकता हूँ।
डीलर-पुश-22 नियम के तहत खिलाड़ी को 6.91% का नुकसान होगा। हालाँकि, डीलर इससे 22 ज़्यादा अंक हासिल करेगा, क्योंकि खिलाड़ी को इस बात से कोई फ़र्क़ नहीं पड़ेगा कि वह पहले बस्ट हुआ है या नहीं। नियमों के अनुसार, खिलाड़ी लगभग 15.7% बार बस्ट होगा। अगर हम मान लें कि यह डीलर के बस्ट होने की संभावना से असंबंधित है (जो कि ऐसा नहीं है), तो डीलर के बस्ट होने की संभावना 6.91%/(1.0-0.157) = 8.2% है।
मुझे पता है कि यह थोड़ा मुश्किल है, लेकिन मान लेते हैं कि खिलाड़ी की 22 की संभावना भी वही है। मुझे पता है कि डीलर खिलाड़ी से ज़्यादा बार बस्ट होगा, लेकिन स्प्लिट के बाद यह कूपन भी नहीं गिना जाता, तो मान लेते हैं कि ये कारक ऑफसेट हो जाते हैं। तो, अगर खिलाड़ी को 8.2% हाथों में 22 मिलता है, तो उसे हर 1/0.082 = औसतन 12.2 हाथों में एक बार 22 मिलेगा।
मान लीजिए कि बेस गेम में हाउस एज 0.75% है। उस हाउस एज पर 12.2 हैंड खेलने की लागत 12.2*0.0075 = 0.0915 है। तो, इसे एक यूनिट वैल्यू से घटाएँ और आपको कूपन का मूल्य 1.0 - 0.0915 मिलेगा, जो अंकित मूल्य का लगभग 91% है।
यह प्रश्न विज़ार्ड ऑफ़ वेगास में मेरे मंच पर उठाया गया है और इस पर चर्चा की गई है।