जादूगर से पूछो #313
हमारे अन्य पाठकों को याद दिला दूँ कि क्लियोपेट्रा केनो पारंपरिक केनो की तरह ही खेला जाता है, सिवाय इसके कि अगर आखिरी गेंद खिलाड़ी की पसंद से मेल खाती है और जीत हासिल होती है, तो खिलाड़ी 2x गुणक के साथ 12 मुफ़्त गेम भी जीतेगा। मुफ़्त गेम से ज़्यादा मुफ़्त गेम नहीं मिलते।
आपने पिक्स की संख्या या पे टेबल नहीं बताई, तो चलिए उदाहरण के तौर पर 3-10-56-180-1000 पिक-8 पे टेबल का इस्तेमाल करते हैं। सबसे पहले, रिटर्न की गणना करते हैं।
केनो में y में से x गेंदें निकालने के तरीकों की संख्या, 20 में से x गेंदें और 60 में से yx गेंदें निकालने के तरीकों की संख्या के बराबर है। एक्सेल में, यह combin(20,x)*combin(60,yx) के बराबर है। एक और अनुस्मारक के रूप में, combin(x,y) = x!/(y!*(xy)!)। अंततः x! = 1*2*3*...*x।
अब जब यह समीक्षा पूरी हो गई है, तो उस भुगतान तालिका की वापसी तालिका यहाँ दी गई है। दाएँ कॉलम में जीत का अपेक्षित वर्ग दिखाया गया है, जिसकी हमें बाद में ज़रूरत पड़ेगी।
पिक 8 केनो
| आयोजन | भुगतान करता है | युग्म | संभावना | वापस करना | वापसी^2 |
|---|---|---|---|---|---|
| 0 | 0 | 2,558,620,845 | 0.088266 | 0.000000 | 0.000000 |
| 1 | 0 | 7,724,138,400 | 0.266464 | 0.000000 | 0.000000 |
| 2 | 0 | 9,512,133,400 | 0.328146 | 0.000000 | 0.000000 |
| 3 | 0 | 6,226,123,680 | 0.214786 | 0.000000 | 0.000000 |
| 4 | 3 | 2,362,591,575 | 0.081504 | 0.244511 | 0.733533 |
| 5 | 10 | 530,546,880 | 0.018303 | 0.183026 | 1.830259 |
| 6 | 56 | 68,605,200 | 0.002367 | 0.132536 | 7.422014 |
| 7 | 180 | 4,651,200 | 0.000160 | 0.028882 | 5.198747 |
| 8 | 1000 | 125,970 | 0.000004 | 0.004346 | 4.345661 |
| कुल | 28,987,537,150 | 1.000000 | 0.593301 | 19.530214 |
अब, औसत बोनस की गणना करते हैं। ऊपर दी गई तालिका से हम देख सकते हैं कि बोनस को छोड़कर, औसत जीत 0.593301 है। बोनस में, खिलाड़ी को 12 दोगुने मुफ़्त स्पिन मिलते हैं। इस प्रकार, बोनस से अपेक्षित जीत 2×12×0.593301 = 14.239212 है।
अब, बोनस जीतने की प्रायिकता की गणना करते हैं। अगर खिलाड़ी चार संख्याएँ पकड़ता है, तो 20वीं गेंद के उन 4 में से एक होने की प्रायिकता 4/20 है। सामान्य तौर पर, अगर खिलाड़ी c पकड़ता है, तो 20वीं गेंद के जीत में योगदान देने की प्रायिकता c/20 है।
बोनस जीतने का सूत्र है: संभावना (कैच 4)*(4/20) + संभावना (कैच 5)*(5/20) + संभावना (कैच 6)*(6/20) + संभावना (कैच 7)*(7/20) + संभावना (कैच 8)*(8/20)। ऊपर दी गई रिटर्न तालिका से हम किसी भी जीत की संभावना जानते हैं। तो, बोनस जीतने की संभावना है:
0.081504*(4/20) + 0.018303*(5/20) + 0.002367*(6/20) + 0.000160*(7/20) + 0.000004*(8/20) = 0.021644.
बोनस जीतने की संभावना और औसत बोनस जीत के साथ, हम बोनस से रिटर्न की गणना 0.021644 × 14.239212 = 0.308198 के रूप में कर सकते हैं।
हमें यह जानने की आवश्यकता नहीं है, लेकिन खेल के लिए कुल रिटर्न, बेस गेम से रिटर्न और बोनस से रिटर्न का योग है, जो 0.593301 + 0.308198 = 0.901498 के बराबर है।
अब, आइए वास्तविक विचरण पर आते हैं। याद दिला दें कि विचरण का एक सामान्य सूत्र है:
var(x + y) = var(x) + var(y) + 2*cov(x,y), जहाँ var प्रसरण को दर्शाता है और cov सहप्रसरण को दर्शाता है। इस खेल के इस मामले में:
कुल विचरण = var(बेस गेम) + var(बोनस) + 2*cov(बेस गेम और बोनस).
विचरण का मूल सूत्र E(x^2) - [E(x)]^2 है। दूसरे शब्दों में, जीत का अपेक्षित वर्ग, अपेक्षित जीत के वर्ग से घटाकर।
तो चलिए, बेस गेम के प्रसरण से शुरुआत करते हैं। याद कीजिए, मैंने पहले कहा था कि हमें पहली तालिका से अपेक्षित जीत का वर्ग चाहिए होगा। उस पहली तालिका के निचले दाएँ कक्ष में अपेक्षित जीत का वर्ग 19.530214 दिखाया गया है। हम पहले से ही जानते हैं कि अपेक्षित जीत 0.593301 है। इस प्रकार, बेस गेम का प्रसरण 19.530214 - 0.593301 2 = 19.178208 है।
अब, बोनस का विचरण (variance) निकालते हैं (यह मानते हुए कि बोनस पहले ही मिल चुका है)। इसके लिए, याद रखें कि:
var(ax) = a 2 x, जहाँ a एक स्थिरांक है।
यह भी याद रखें कि n यादृच्छिक चर x का प्रसरण nx है।
जैसा कि कहा गया है, यदि बोनस गेम में आधार जीत x है, तो पूरे बोनस का प्रसरण 2 2 × 12 × x है। जैसा कि हम ऊपर से जानते हैं, बोनस को छोड़कर, आधार गेम में एक स्पिन का प्रसरण 19.178208 के बराबर है। इसलिए, बोनस का प्रसरण, बशर्ते कि बोनस पहले ही हिट हो चुका हो, 2 2 × 12 × 19.178208 = 920.554000 है।
हालाँकि, हमें पहली गेंद निकाले जाने से पहले बोनस का प्रसरण जानना होगा, जिसमें बोनस के न जीतने की संभावना भी शामिल है। नहीं, हम बोनस के प्रसरण को उसके जीतने की प्रायिकता से गुणा नहीं कर सकते। इसके बजाय, याद रखें कि var(x) = E(x^2) - [E(x)]^2। आइए इसे इस प्रकार पुनर्व्यवस्थित करें:
ई(x^2) = var(x) + [ई(x)]^2
हम बोनस का माध्य और विचरण जानते हैं, इसलिए बोनस में अपेक्षित जीत का वर्ग 920.554000 + 19.178208 2 = 1123.309169 है।
इसलिए, पहली गेंद निकाले जाने से पहले बोनस से जीत का अपेक्षित वर्ग, प्रायः (बोनस) × E(x^2) = 0.021644 × 1123.309169 = 24.313239 है।
हमने पहले ही गणना कर ली है कि पहली गेंद से पहले बोनस से अपेक्षित जीत 0.308198 है। इसलिए, पहली गेंद से पहले बोनस का कुल विचरण 24.313239 - 0.308198 2 = 24.218253 है।
अगला चरण सहप्रसरण की गणना करना है। आप पूछ सकते हैं, "आधार जीत और बोनस जीत के बीच सहसंबंध क्यों है?" ऐसा इसलिए है क्योंकि बोनस को ट्रिगर करने के लिए खींची गई आखिरी गेंद का जीत में योगदान होना ज़रूरी है। यह मानते हुए कि आखिरी गेंद ने जीत में योगदान दिया है, औसत जीत बढ़ जाती है। याद दिला दें कि बेयस का स्थिति प्रायिकता सूत्र कहता है:
P(A दिया गया B) = P(A और B)/P(B).
अब हम बेस गेम के लिए अपनी रिटर्न तालिका को पुनः तैयार करते हैं, यह देखते हुए कि अंतिम गेंद हिट थी:
अंतिम गेंद पर हिट होने पर 8 केनो चुनें
| आयोजन | भुगतान करता है | युग्म | संभावना | वापस करना |
|---|---|---|---|---|
| 0 | 0 | - | 0.000000 | 0.000000 |
| 1 | 0 | - | 0.000000 | 0.000000 |
| 2 | 0 | - | 0.000000 | 0.000000 |
| 3 | 0 | - | 0.000000 | 0.000000 |
| 4 | 3 | 472,518,315 | 0.753119 | 2.259358 |
| 5 | 10 | 132,636,720 | 0.211402 | 2.114019 |
| 6 | 56 | 20,581,560 | 0.032804 | 1.837010 |
| 7 | 180 | 1,627,920 | 0.002595 | 0.467036 |
| 8 | 1000 | 50,388 | 0.000080 | 0.080310 |
| कुल | 627,414,903 | 1.000000 | 6.757734 |
नीचे के दाहिने सेल से पता चलता है कि यह मानते हुए कि अंतिम गेंद हिट थी, औसत जीत 6.757734 है।
इसके बाद, अपने कॉलेज की सांख्यिकी कक्षा से याद करें कि:
cov(x,y) = exp(xy) - exp(x)*exp(y) .
हमारे मामले में, मान लीजिए x = बेस गेम जीत और y = बोनस जीत। आइए पहले exp(xy) पर काम करें।
Exp(xy) = prob(बोनस जीता)*(औसत बेस गेम जीत, बोनस जीता दिया गया)*औसत(बोनस जीत) + prob(बोनस नहीं जीता)*(औसत बेस गेम जीत, बोनस नहीं जीता दिया गया)*औसत(बोनस जीत, बोनस नहीं जीता दिया गया)। यह कहना आसान है कि औसत(बोनस जीत, बोनस नहीं जीता दिया गया) = 0, इसलिए हम इसे इस प्रकार लिख सकते हैं:
Exp(xy) = prob(बोनस जीता)*(औसत बेस गेम जीत दिया गया बोनस जीता)*औसत(बोनस जीत) =
0.021644 × 6.757734 × 14.239212 = 2.082719.हमने पहले ही E(x) और E(y) के लिए हल निकाल लिया है, इसलिए सहप्रसरण है:
cov(x,y) = exp(xy) - exp(x)*exp(y) = 2.082719 - 0.593301 × 0.308198 = 1.899865।
आइए सहप्रसरण के मामले में विचरण के समग्र समीकरण पर वापस जाएं:
कुल विचरण = var(बेस गेम) + var(बोनस) + 2*cov(बेस गेम और बोनस) = 19.178208 + 24.218253 + 2×1.899865 = 47.196191. मानक विचलन इसका वर्गमूल है, जो 6.869948 है।
तो लीजिए, लीजिए। इसमें मुझे घंटों लग गए, तो उम्मीद है आप खुश होंगे।
यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।
मैंने सुना है कि संयुक्त राज्य अमेरिका में आमतौर पर 50% बताई गई एक शादी के तलाक में खत्म होने की संभावना, उसी समयावधि में हुई शादियों की संख्या के मुकाबले तलाक की संख्या के आधार पर निकाली जाती है। क्या यह सच है? क्या आपको लगता है कि यह आँकड़ा निकालने का उचित तरीका है? मैं इस पर सवाल उठा रहा हूँ क्योंकि आप लंबे समय में हुई शादियों की तुलना में कम समय में हुए तलाक को देख रहे हैं।
यदि जनसंख्या और आयु वितरण स्थिर थे, और तलाक की संभावना वास्तव में 50% थी, तो हम बड़े नमूने के आकार को देखते हुए, किसी भी समयावधि में दो विवाहों के मुकाबले एक तलाक का अनुपात देखने की उम्मीद करेंगे।
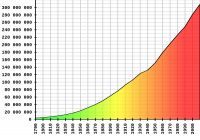
हालाँकि, जनसंख्या स्थिर नहीं है। इस ग्राफ़ से ऐसा लगता है कि अमेरिका की जनसंख्या प्रति दशक 10.71% की दर से बढ़ रही है। यानी प्रति वर्ष 1.02%। इसे सरल रखने के लिए हम इसे केवल 1% ही मानेंगे।
मानचित्र स्रोत: अमेरिकी जनगणना
फादरली डॉट कॉम के अनुसार, असफल विवाह की औसत अवधि 8 वर्ष होती है।
यदि आप वर्तमान में विवाहों की तुलना में तलाक का अनुपात 1:2 पर देख रहे हों, तो किसी भी विवाह के तलाक में समाप्त होने की औसत संभावना क्या होगी?
अभी हम जो तलाक देख रहे हैं, वे 8 साल पहले हुई शादियों से हैं, जब जनसंख्या आज की तुलना में 92.35% थी। सरल गणित बताता है कि तलाक की वास्तविक संभावना 54.14% है।
आइये इसकी जांच करें।
सबसे पहले, सीडीसी के अनुसार, प्रति वर्ष प्रति 1000 जनसंख्या पर 6.9 विवाह होते हैं। यह आँकड़ा इस प्रश्न से संबंधित नहीं है, लेकिन मुझे लगता है कि इससे संबंधित संख्याओं को समझने में मदद मिलती है।
मान लीजिए 8 साल पहले जनसंख्या 300,000,000 थी। तो उस साल 0.69% * 300 मिलियन = 2,070,000 शादियाँ हुईं।
यदि आठ वर्ष बाद उनमें से 54.14% तलाक में परिणत होते हैं, तो वर्तमान में हम 2,070,000 * 54.14% = 1,120,698 तलाक देख रहे होंगे।
1,120,698 / 2,070,000 = वर्तमान में विवाह की तुलना में तलाक का 50% अनुपात देखा गया।
कहीं कोई यह न कह दे, हाँ, मुझे पता है कि सभी तलाक ठीक आठ साल में खत्म नहीं होते। फिर भी, सभी बातों को ध्यान में रखते हुए, मैं कहता हूँ कि अंतिम परिणाम मेरे 54.14% वास्तविक तलाक दर से ज़्यादा दूर नहीं होगा।
यह प्रश्न विज़ार्ड ऑफ़ वेगास में मेरे मंच पर उठाया गया है और इस पर चर्चा की गई है।
आपके 100 कर्मचारियों का कार्यालय एक सीक्रेट सांता उपहार विनिमय करता है। इसमें आप कागज़ के अलग-अलग टुकड़ों पर सबके नाम लिखते हैं, उन्हें एक टोपी में डालते हैं, और हर कोई उपहार देने के लिए यादृच्छिक रूप से एक नाम चुनता है।
सवाल यह है कि औसतन कितने बंद लूप होंगे? उदाहरण के लिए, बंद लूप में गॉर्डन डॉन को देता है, जो जॉन को देता है, जो नाथन को देता है, जो गॉर्डन को देता है। या फिर अपना नाम खुद बनाना।
मान लीजिए कि हर कोई एक-एक करके एक ही चीज़ चुनता है। जैसे-जैसे हर व्यक्ति चुनता जाएगा, दो तरह की स्थितियाँ पैदा होंगी:
- चुनने वाले का नाम पहले ही चुन लिया गया है।
- चुनने वाले का नाम अभी भी नामों की टोकरी में है।
किसी भी चयनकर्ता के लिए, मान लीजिए कि चुनने के लिए n लोग बचे हैं।
अगर चुनने वाले का नाम पहले ही चुन लिया गया है, तो 1/n संभावना है कि चुनने वाला अपने नाम से जुड़े लूप को बंद कर देगा। उदाहरण के लिए, मान लीजिए एमी चुन रही है। एमी का नाम पहले से ही बॉब के पास है, बॉब का नाम पहले से ही चार्ली के पास है, और चार्ली का नाम अभी भी बिन में है। बिन में अभी भी n नाम होने पर, एमी द्वारा चार्ली का नाम चुनने की 1/n संभावना है, जिससे लूप बंद हो जाता है।
यदि चुनने वाले का नाम पहले से नहीं चुना गया है, तो 1/n संभावना है कि एमी अपना नाम चुन ले, जिससे लूप बंद हो जाएगा।
किसी भी तरह, अगर पिकर लूप बंद नहीं करता, तो वह एक और चेन का हिस्सा जोड़ रहा होता है, जिसे अंततः कोई और बंद कर देगा। हर चेन को सिर्फ़ एक बार ही गिना जाना चाहिए, जब वह बंद हो जाए।
इस प्रकार उत्तर है 1/100 + 1/99 + 1/98 + ... + 1/1 =~ 5.187377518.
खिलाड़ियों की किसी भी पर्याप्त बड़ी संख्या, n, के लिए अनुमान ln(n) है।
यह प्रश्न मेरे फोरम विजार्ड ऑफ वेगास में पूछा गया है और इस पर चर्चा की गई है।
एक वीडियो स्लॉट मशीन खेलने के लिए एक अतिरिक्त गारंटीकृत वाइल्ड का मूल्य कितना होगा?
यह कई बातों पर निर्भर करता है। मैं आपके प्रश्न की व्याख्या इस प्रकार करूँगा कि खिलाड़ी को सामान्यतः मिलने वाली औसत संख्या से ऊपर एक अतिरिक्त वाइल्ड का मूल्य क्या है। हालाँकि इसका उत्तर हर खेल में काफ़ी अलग-अलग होगा, लेकिन एक महत्वपूर्ण कारक स्क्रीन पर पंक्तियों की संख्या है। अगर तीन पंक्तियाँ हैं, तो अतिरिक्त वाइल्ड से 1/3 पेलाइन्स को फ़ायदा होगा। इसी तरह, अगर चार पंक्तियाँ हैं, तो इसका मूल्य कम होगा और यह 1/4 पेलाइन्स को प्रभावित करेगा।
आपके प्रश्न का उत्तर देने के लिए, मैंने क्लियोपेट्रा गेम देखा, जिसका मैंने पहले ही विश्लेषण कर लिया है। नीचे दी गई तालिका, वाइल्ड की एक यादृच्छिक संख्या की तुलना में, वाइल्ड के अपेक्षित मान में वृद्धि दर्शाती है।
क्लियोपेट्रा में एक्स्ट्रा वाइल्ड का मूल्य
| रील | 3 पंक्तियाँ | 4 पंक्तियाँ |
|---|---|---|
| 1 | 95.71% | 71.79% |
| 2 | 99.76% | 74.82% |
| 3 | 76.24% | 57.18% |
| 4 | 21.25% | 15.93% |
| 5 | 1.96% | 1.47% |