जादूगर से पूछो #307
मैं 2018 के "डेड पूल" में भाग ले रहा हूँ। नियम ये हैं:
- प्रत्येक खिलाड़ी को 100 वर्ष से कम आयु के दस जीवित हस्तियों की सूची प्रस्तुत करनी होगी।
- यदि किसी सेलिब्रिटी की मृत्यु हो जाती है, जैसा कि एसोसिएटेड प्रेस द्वारा उल्लेख किया गया है, 2018 में, तो उस सेलिब्रिटी का नाम अपनी सूची में रखने वाले किसी भी व्यक्ति को 100-x अंक प्राप्त होंगे, जहां x मृत्यु की आयु है।
- 1/1/2019 को सबसे अधिक अंक वाला खिलाड़ी जीतता है।
औसत के आधार पर, इस खेल के लिए इष्टतम रणनीति क्या है?
एक पूर्व एक्चुअरी होने के नाते, आपने बिल्कुल सही सवाल पूछा है। उम्मीद है कि एक्चुअरी सोसाइटी मेरे जवाब को पेशे का दुरुपयोग नहीं मानेगी। बहरहाल, आपके सवाल का जवाब देने के लिए मैंने अपने पूर्व कार्यस्थल, सामाजिक सुरक्षा प्रशासन के मुख्य एक्चुअरी कार्यालय, की 2014 की जीवन-अवधि तालिका देखी।
एक अवधि जीवन तालिका, अन्य बातों के अलावा, 2014 में किसी भी आयु और लिंग के व्यक्ति की मृत्यु की संभावना को दर्शाती है। उस जानकारी का उपयोग करके मैंने निम्नलिखित तालिका बनाई है, जो 0 से 100 तक की सभी आयु और दोनों लिंगों के लिए मृत्यु की संभावना और अपेक्षित अंक दोनों को दर्शाती है।
2014 अवधि जीवन तालिका मृत्यु पूल
| आयु | की संभावना मृत्यु — पुरुष | की संभावना मृत्यु — महिला | अपेक्षित अंक — पुरुष | अपेक्षित अंक — महिला |
|---|---|---|---|---|
| 0 | 0.006320 | 0.005310 | 0.632000 | 0.531000 |
| 1 | 0.000403 | 0.000352 | 0.039852 | 0.034835 |
| 2 | 0.000282 | 0.000221 | 0.027626 | 0.021683 |
| 3 | 0.000211 | 0.000161 | 0.020514 | 0.015612 |
| 4 | 0.000181 | 0.000131 | 0.017405 | 0.012556 |
| 5 | 0.000161 | 0.000111 | 0.015313 | 0.010515 |
| 6 | 0.000141 | 0.000111 | 0.013260 | 0.010405 |
| 7 | 0.000131 | 0.000101 | 0.012184 | 0.009360 |
| 8 | 0.000121 | 0.000091 | 0.011127 | 0.008334 |
| 9 | 0.000091 | 0.000081 | 0.008256 | 0.007328 |
| 10 | 0.000101 | 0.000091 | 0.009073 | 0.008154 |
| 11 | 0.000101 | 0.000081 | 0.008973 | 0.007168 |
| 12 | 0.000131 | 0.000101 | 0.011535 | 0.008861 |
| 13 | 0.000202 | 0.000131 | 0.017547 | 0.011389 |
| 14 | 0.000303 | 0.000151 | 0.026023 | 0.012992 |
| 15 | 0.000404 | 0.000191 | 0.034304 | 0.016267 |
| 16 | 0.000505 | 0.000232 | 0.042393 | 0.019464 |
| 17 | 0.000616 | 0.000272 | 0.051129 | 0.022582 |
| 18 | 0.000748 | 0.000302 | 0.061316 | 0.024796 |
| 19 | 0.000880 | 0.000343 | 0.071262 | 0.027768 |
| 20 | 0.001022 | 0.000373 | 0.081780 | 0.029855 |
| 21 | 0.001145 | 0.000404 | 0.090445 | 0.031884 |
| 22 | 0.001258 | 0.000444 | 0.098105 | 0.034643 |
| 23 | 0.001310 | 0.000475 | 0.100880 | 0.036546 |
| 24 | 0.001332 | 0.000495 | 0.101246 | 0.037625 |
| 25 | 0.001344 | 0.000526 | 0.100811 | 0.039422 |
| 26 | 0.001377 | 0.000556 | 0.101864 | 0.041162 |
| 27 | 0.001389 | 0.000577 | 0.101371 | 0.042106 |
| 28 | 0.001421 | 0.000608 | 0.102330 | 0.043740 |
| 29 | 0.001454 | 0.000648 | 0.103234 | 0.046036 |
| 30 | 0.001507 | 0.000669 | 0.105517 | 0.046837 |
| 31 | 0.001530 | 0.000710 | 0.105584 | 0.048998 |
| 32 | 0.001574 | 0.000751 | 0.107011 | 0.051084 |
| 33 | 0.001617 | 0.000813 | 0.108364 | 0.054454 |
| 34 | 0.001661 | 0.000864 | 0.109644 | 0.057041 |
| 35 | 0.001716 | 0.000926 | 0.111521 | 0.060194 |
| 36 | 0.001781 | 0.001008 | 0.113970 | 0.064538 |
| 37 | 0.001857 | 0.001081 | 0.116963 | 0.068090 |
| 38 | 0.001933 | 0.001164 | 0.119830 | 0.072145 |
| 39 | 0.002020 | 0.001237 | 0.123207 | 0.075427 |
| 40 | 0.002118 | 0.001340 | 0.127066 | 0.080422 |
| 41 | 0.002258 | 0.001445 | 0.133232 | 0.085232 |
| 42 | 0.002410 | 0.001560 | 0.139778 | 0.090455 |
| 43 | 0.002615 | 0.001696 | 0.149075 | 0.096649 |
| 44 | 0.002843 | 0.001853 | 0.159228 | 0.103761 |
| 45 | 0.003105 | 0.002011 | 0.170771 | 0.110606 |
| 46 | 0.003401 | 0.002191 | 0.183635 | 0.118300 |
| 47 | 0.003742 | 0.002403 | 0.198314 | 0.127342 |
| 48 | 0.004108 | 0.002647 | 0.213613 | 0.137656 |
| 49 | 0.004532 | 0.002894 | 0.231133 | 0.147577 |
| 50 | 0.004994 | 0.003194 | 0.249696 | 0.159718 |
| 51 | 0.005473 | 0.003487 | 0.268191 | 0.170880 |
| 52 | 0.005993 | 0.003794 | 0.287656 | 0.182103 |
| 53 | 0.006565 | 0.004104 | 0.308561 | 0.192871 |
| 54 | 0.007159 | 0.004428 | 0.329324 | 0.203676 |
| 55 | 0.007799 | 0.004767 | 0.350946 | 0.214498 |
| 56 | 0.008475 | 0.005153 | 0.372902 | 0.226729 |
| 57 | 0.009179 | 0.005534 | 0.394696 | 0.237972 |
| 58 | 0.009856 | 0.005889 | 0.413944 | 0.247347 |
| 59 | 0.010575 | 0.006272 | 0.433558 | 0.257150 |
| 60 | 0.011350 | 0.006683 | 0.453991 | 0.267338 |
| 61 | 0.012209 | 0.007180 | 0.476135 | 0.280016 |
| 62 | 0.013061 | 0.007720 | 0.496330 | 0.293355 |
| 63 | 0.013921 | 0.008339 | 0.515084 | 0.308537 |
| 64 | 0.014814 | 0.009029 | 0.533320 | 0.325041 |
| 65 | 0.015831 | 0.009839 | 0.554094 | 0.344371 |
| 66 | 0.016981 | 0.010741 | 0.577354 | 0.365197 |
| 67 | 0.018300 | 0.011752 | 0.603909 | 0.387812 |
| 68 | 0.019778 | 0.012879 | 0.632894 | 0.412117 |
| 69 | 0.021443 | 0.014142 | 0.664734 | 0.438397 |
| 70 | 0.023384 | 0.015613 | 0.701513 | 0.468376 |
| 71 | 0.025547 | 0.017271 | 0.740873 | 0.500852 |
| 72 | 0.027877 | 0.019047 | 0.780560 | 0.533320 |
| 73 | 0.030384 | 0.020918 | 0.820374 | 0.564797 |
| 74 | 0.033098 | 0.022938 | 0.860535 | 0.596385 |
| 75 | 0.036256 | 0.025299 | 0.906400 | 0.632465 |
| 76 | 0.039868 | 0.028043 | 0.956841 | 0.673035 |
| 77 | 0.043883 | 0.031127 | 1.009299 | 0.715914 |
| 78 | 0.048257 | 0.034590 | 1.061657 | 0.760984 |
| 79 | 0.053128 | 0.038456 | 1.115692 | 0.807583 |
| 80 | 0.058709 | 0.043007 | 1.174177 | 0.860145 |
| 81 | 0.065070 | 0.048186 | 1.236322 | 0.915536 |
| 82 | 0.072149 | 0.053762 | 1.298691 | 0.967712 |
| 83 | 0.079906 | 0.059769 | 1.358409 | 1.016065 |
| 84 | 0.088524 | 0.066380 | 1.416378 | 1.062085 |
| 85 | 0.098157 | 0.073823 | 1.472348 | 1.107351 |
| 86 | 0.108904 | 0.082381 | 1.524651 | 1.153334 |
| 87 | 0.120889 | 0.092180 | 1.571556 | 1.198344 |
| 88 | 0.134134 | 0.103305 | 1.609607 | 1.239664 |
| 89 | 0.148707 | 0.115744 | 1.635778 | 1.273180 |
| 90 | 0.164522 | 0.129477 | 1.645220 | 1.294772 |
| 91 | 0.181584 | 0.144435 | 1.634254 | 1.299911 |
| 92 | 0.199903 | 0.160621 | 1.599225 | 1.284970 |
| 93 | 0.219362 | 0.177816 | 1.535534 | 1.244713 |
| 94 | 0.239881 | 0.196194 | 1.439286 | 1.177165 |
| 95 | 0.260293 | 0.214694 | 1.301463 | 1.073469 |
| 96 | 0.280129 | 0.233056 | 1.120515 | 0.932225 |
| 97 | 0.299042 | 0.251152 | 0.897125 | 0.753456 |
| 98 | 0.316317 | 0.268235 | 0.632634 | 0.536471 |
| 99 | 0.332667 | 0.284442 | 0.332667 | 0.284442 |
| 100 | 0.348651 | 0.301417 | 0.000000 | 0.000000 |
तालिका से पता चलता है कि 90 वर्षीय व्यक्ति के लिए अधिकतम अपेक्षित अंक 1.645220 है।
यह प्रश्न मेरे गैर-जुआ मंच, डाइवर्सिटी टुमॉरो में उठाया गया है और इस पर चर्चा की गई है।
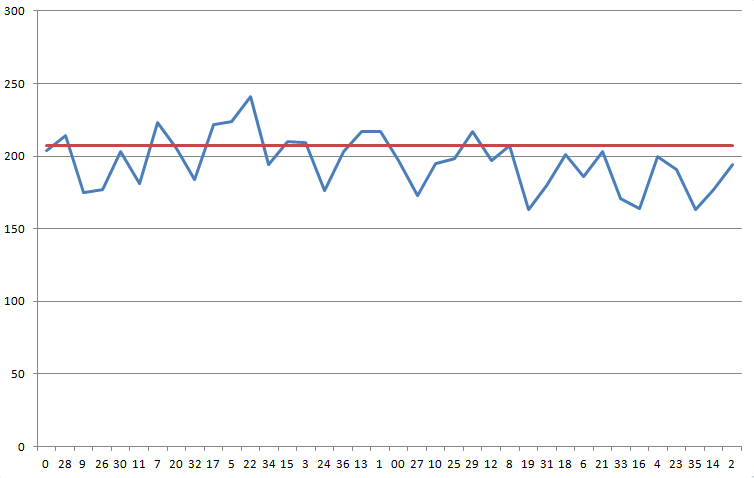
मैंने रूलेट में 7,456 स्पिन रिकॉर्ड किए। परिणाम इस प्रकार हैं। मुझे संदेह है कि पहिया पक्षपाती है, लेकिन मुझे यकीन नहीं है कि डेटा इसे खेलने के लिए पर्याप्त निर्णायक है या नहीं।
रूलेट डेटा
| जीत संख्या | पुनरावृत्तियां |
|---|---|
| 0 | 204 |
| 28 | 214 |
| 9 | 175 |
| 26 | 177 |
| 30 | 203 |
| 11 | 181 |
| 7 | 223 |
| 20 | 205 |
| 32 | 184 |
| 17 | 222 |
| 5 | 224 |
| 22 | 241 |
| 34 | 194 |
| 15 | 210 |
| 3 | 209 |
| 24 | 176 |
| 36 | 203 |
| 13 | 217 |
| 1 | 217 |
| 00 | 197 |
| 27 | 173 |
| 10 | 195 |
| 25 | 198 |
| 29 | 217 |
| 12 | 197 |
| 8 | 207 |
| 19 | 163 |
| 31 | 180 |
| 18 | 201 |
| 6 | 186 |
| 21 | 203 |
| 33 | 171 |
| 16 | 164 |
| 4 | 200 |
| 23 | 191 |
| 35 | 163 |
| 14 | 177 |
| 2 | 194 |
| कुल | 7456 |
निम्नलिखित ग्राफ़ आपके परिणामों को पहिये पर क्रमिक क्रम में दर्शाता है। नीली रेखा आपके परिणाम दिखाती है। लाल रेखा वह संख्या है जिसकी आपको 5.26% हाउस एज को पार करने के लिए आवश्यकता है, 207.11।
इस वितरण पर काई-स्क्वेयर परीक्षण से 37 डिग्री स्वतंत्रता के साथ 68.1 का आँकड़ा प्राप्त होता है। इस विषम या उससे अधिक परिणाम की संभावना 725 में 1 है।
मुझे नहीं लगता कि इस स्थिति के लिए काई-स्क्वेयर्ड सही परीक्षण है क्योंकि यह परिणामों के क्रम पर विचार नहीं करता, लेकिन मुझे इससे बेहतर कोई परीक्षण नहीं पता। कुछ लोगों ने कोल्मोगोरोव-स्मिरनोव परीक्षण का सुझाव दिया है, लेकिन मुझे नहीं लगता कि वह उपयुक्त है। अगर कोई और उपयुक्त परीक्षण हैं, तो मैं पूरी तरह तैयार हूँ।
मैं कह सकता हूँ कि अगर आपने 5 नंबर के आसपास 3-अंकीय चाप पर दांव लगाया होता, तो आपको अपने रिकॉर्ड किए गए स्पिन पर 10.57% का लाभ होता। हालाँकि, अगर आपने इसे 7-अंकीय चाप तक बढ़ा दिया, तो यह लाभ घटकर 2.84% रह जाता है।
अगर मुझे सीधे-सादे अंग्रेजी में जवाब देने के लिए मजबूर किया जाए, तो मैं कहूँगा कि पहिया इस बात का सबूत ज़रूर देता है, लेकिन किसी भी तरह के संदेह से परे कोई सबूत नहीं कि पहिया पक्षपाती है। हालाँकि, यह पक्षपात शायद हाउस एज पर पूरी तरह से और आत्मविश्वास से काबू पाने के लिए पर्याप्त नहीं है। यह मानते हुए कि कैसीनो टेबलों के बीच पहियों को नहीं बदलता, मैं कहूँगा कि बड़ी रकम दांव पर लगाने से पहले ज़्यादा जानकारी इकट्ठा कर लेनी चाहिए। मुझे खेद है कि यह जवाब इतना अस्पष्ट है।
यह प्रश्न विज़ार्ड ऑफ़ वेगास में मेरे मंच पर उठाया गया है और इस पर चर्चा की गई है।
दो खिलाड़ियों, सैम और डैन, के पास पाँच-पाँच सिक्के हैं। दोनों को अपने हाथ में एक से पाँच सिक्के रखने का चुनाव करना होगा। साथ ही, प्रत्येक को खेले गए सिक्कों की संख्या भी बतानी होगी। अगर दोनों समान संख्या में सिक्के चुनते हैं, तो सैम जीत जाएगा और खेले गए सभी सिक्के ले लेगा। अगर दोनों अलग-अलग संख्या में सिक्के चुनते हैं, तो डैन खेले गए सभी सिक्के ले लेगा। यह मानते हुए कि दोनों खिलाड़ी पूर्ण तर्कशास्त्री हैं, डैन के लिए सर्वोत्तम रणनीति क्या है?
डैन को अपनी रणनीति इस प्रकार बनानी चाहिए:
- एक सिक्का चुनने की संभावना = 77/548.
- एक सिक्का चुनने की संभावना = 107/548.
- एक सिक्का चुनने की संभावना = 117/548.
- एक सिक्का चुनने की संभावना = 122/548.
- एक सिक्का चुनने की संभावना = 125/548.
इस रणनीति के साथ, डैन हर बार 3.640510949 सिक्के जीतने की उम्मीद कर सकता है, चाहे सैम कितने भी सिक्के उठाए।
इसका समाधान मेरी गणित समस्या साइट, समस्या 230 पर पाया जा सकता है।
इससे संबंधित एक प्रश्न, जिसके कारण यह प्रश्न उठा, विज़ार्ड ऑफ़ वेगास पर मेरे फोरम में पाया जा सकता है।
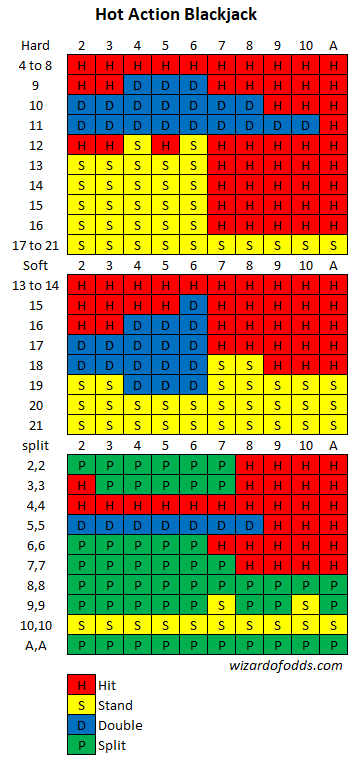
सैन फ़्रांसिस्को के कैलिफ़ोर्निया ग्रैंड कैसीनो में हॉट एक्शन ब्लैकजैक नामक एक ब्लैकजैक गेम खेला जाता है। इस खेल के नियम इस प्रकार हैं:
- एक सतत शफलर में छह डेक, 2 अंकित मूल्य वाले अतिरिक्त 18 जोकर के साथ।
- डीलर ने सॉफ्ट 17 मारा।
- किसी भी पहले 2 कार्ड पर डबल।
- चार हाथों तक पुनः विभाजित करें।
- इक्कों को पुनः विभाजित या ड्रा नहीं किया जाएगा।
- कोई आत्मसमर्पण नहीं।
- ब्लैकजैक 6 से 5 का भुगतान करता है।
- यदि खिलाड़ी के पहले दो कार्ड जोकर हैं, तो उसे 4 से 1 का बोनस मिलता है।
- यदि खिलाड़ी के पहले दो कार्ड सूटेड इक्के हैं, तो उसे 5 से 1 बोनस मिलता है।
- खिलाड़ी को खेलने के लिए 5% कमीशन देना होगा।
मूल रणनीति और हाउस एज क्या है?
सबसे पहले, इन नियमों के अंतर्गत मेरी बुनियादी रणनीति यह है:
कुल मिलाकर, मैं शुरुआती दांव के आधार पर 6.01% (ओह!) का हाउस एज दिखा रहा हूँ। दूसरे शब्दों में, अगर खिलाड़ी $5 कमीशन को छोड़कर $100 का दांव लगाता है, तो उसे $6.01 का नुकसान हो सकता है। इससे पता चलता है कि मैं कैलिफ़ोर्निया में प्लेयर-बैंकिंग वाले खेलों से क्यों दूर रहूँगा, जब तक कि आप खुद बैंकिंग न कर रहे हों।
यह प्रश्न विज़ार्ड ऑफ़ वेगास में मेरे मंच पर उठाया गया है और इस पर चर्चा की गई है।