WOO logo

विज़ार्ड अनुशंसा करता है

जादूगर से पूछो #301

स्थानीय कैसीनो में हर सप्ताह एक पुरस्कार ड्रा होता है, जिसमें विजेता को 5,000 डॉलर नकद या निम्नलिखित पुरस्कारों में से एक वाला रहस्यमय बैग चुनने का विकल्प दिया जाता है:

  • 2,000 डॉलर नकद
  • $4,000 के गैर-परक्राम्य चिप्स
  • $6,000 के गैर-परक्राम्य चिप्स
  • 8,000 डॉलर नकद
  • 10,000 डॉलर नकद


आप क्या चुनेंगे और क्यों?

babyyeespoppy

सबसे पहले, मेरा मानना है कि "गैर-परक्राम्य चिप्स" तब तक इस्तेमाल करने वाले होते हैं जब तक आप हार न जाएँ। इनका मूल्य अंकित मूल्य का लगभग 98% होता है, जो उन खेलों के नियमों पर निर्भर करता है जिनमें आप इन्हें इस्तेमाल कर सकते हैं।

वैसे, औसत बैग की कीमत $5,960 है। यह नकद प्रस्ताव से लगभग 20% ज़्यादा है। इसे पैसे की उपयोगिता की समस्या के रूप में भी देखें, तो आपको बैग लेना ही चाहिए, भले ही आपके पास और कोई संपत्ति न हो।

यह प्रश्न विज़ार्ड ऑफ़ वेगास में मेरे मंच पर पूछा गया और इस पर चर्चा की गई।

योग को 1 के बराबर करने के लिए 0 से 1 तक एक समान वितरण से आपको ड्रॉ की औसत संख्या कितनी चाहिए होगी?

गुमनाम

उत्तर:

[स्पॉइलर] उत्तर है e = 2.7182818....[/स्पॉइलर]

समाधान:

यहाँ समाधान है.


फिल्म गुड विल हंटिंग में चॉकबोर्ड पर गणित की समस्या क्या थी?

गुमनाम

यह वास्तव में काफी आसान था, खासकर एमआईटी में संयोजन गणित के पाठ्यक्रम के लिए। समस्या का शब्दांकन इस प्रकार है:

"आकार n=10 के सभी समरूपी अपरिवर्तनीय वृक्ष बनाएं।"

मैं इसे सरल एवं सादी अंग्रेजी में कहने का प्रयास कर रहा हूँ।

केवल सीधी रेखाओं का उपयोग करके, वे सभी आकृतियाँ बनाएँ जहाँ प्रतिच्छेदों और मृत सिरों का योग 10 के बराबर हो। आपके पास कोई बंद लूप नहीं होना चाहिए। आपके पास दो समतुल्य आकृतियाँ भी नहीं होनी चाहिए। किसी भी प्रतिच्छेदन से कम से कम तीन रास्ते निकलने चाहिए।

आप पूछेंगे, "समतुल्य" से मेरा क्या मतलब है? इसका मतलब है कि आप टुकड़ों को, उनके प्रतिच्छेदन को छोड़कर, अपनी इच्छानुसार किसी भी तरह हिला सकते हैं और इससे कोई नई आकृतियाँ नहीं बनेंगी।

यहाँ एक उदाहरण है: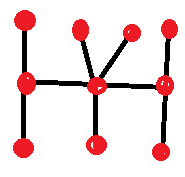



मैं तुम्हें एक इशारा देता हूँ। फिल्म में दिए गए जवाब के उलट, यहाँ दस हैं। विल को सिर्फ़ आठ मिले। देखो, क्या तुम विल हंटिंग की बराबरी कर सकते हो या उसे हरा सकते हो।

[बिगाड़ने वाला]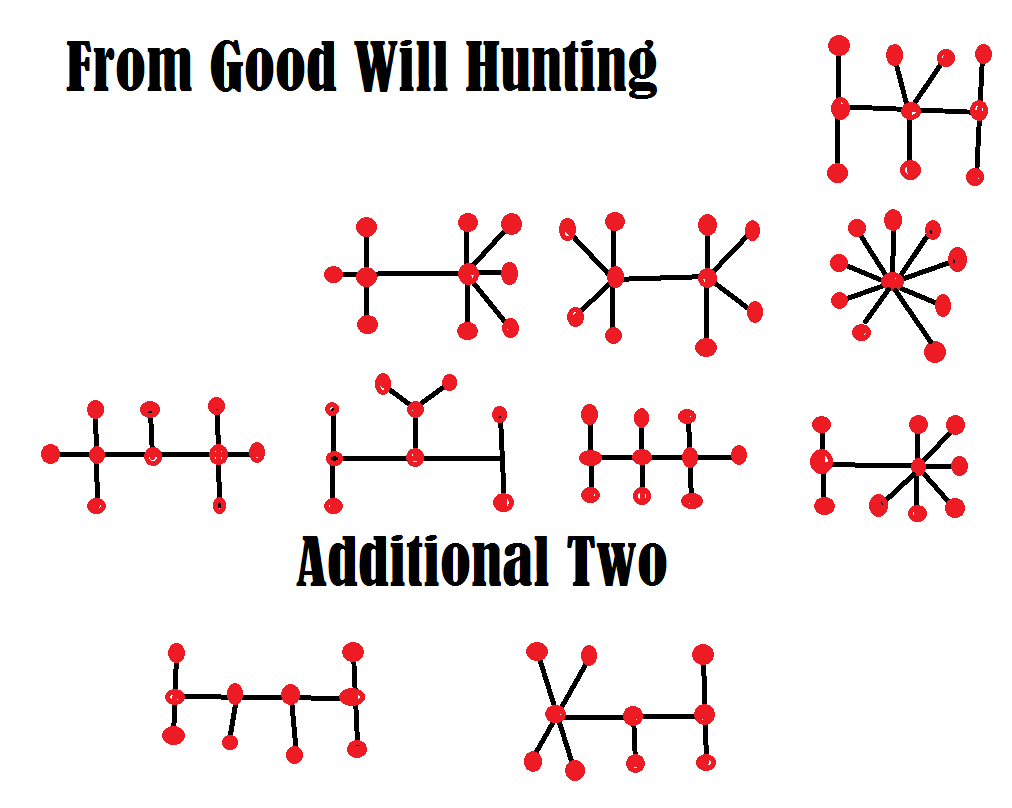

मैं अपनी MathProblems.info साइट पर समस्या 220 पर सभी दस प्रश्नों को हल करने के लिए अपना तर्क प्रस्तुत करता हूँ।

[/spoiler] आगे पढ़ें:



मेक्सिको के कुछ कसीनो में रूलेट में पहिये की जगह पासे का इस्तेमाल होता है। नियम ये हैं:

  • चार पासे हैं - दो हरे, एक लाल और एक नीला।
  • यदि दोनों हरे पासे एक ही स्थान पर आते हैं, तो "स्पिन" का परिणाम शून्य होगा।
  • यदि दोनों हरे पासे छह पर आते हैं, तो "स्पिन" का परिणाम दोहरा शून्य होगा।
  • यदि हरे पासे के साथ कोई अन्य परिणाम आता है, तो लाल और नीले पासे के 36 संभावित परिणामों को "स्पिन" का प्रतिनिधित्व करने के लिए संख्या 1 और 36 से मैप किया जाएगा।


पारंपरिक रूलेट की तुलना में इससे बाधाओं में क्या परिवर्तन होता है?

गुमनाम

0 और 00 के जीतने की संभावना 1/36 होगी। अगर इन नतीजों पर दांव लगाने वालों को सामान्य 35 से 1 का भुगतान मिलता है, तो हाउस एज ठीक 0% होगा।

किसी भी अन्य संख्या के जीतने की संभावना (34/36)*(1/36) = 2.62% होगी। इसकी तुलना पारंपरिक डबल-ज़ीरो रूलेट में 1/38 = 2.63% से करें। 1 से 36 तक की संख्याओं पर किसी भी दांव पर हाउस एज 5.56% होगा। इसकी तुलना पारंपरिक डबल-ज़ीरो रूलेट में 5.26% से करें। इस खेल में मेरी सलाह है कि केवल शून्य और डबल-ज़ीरो पर ही दांव लगाएँ।

यदि कोई इन नियमों की पुष्टि या खंडन कर सकता है और भुगतान कर सकता है, तो कृपया मुझे बताएं।