जादूगर से पूछो #270
मैं एक ऐसे कैसीनो में खेलता हूँ जो आपको असीमित बार जोड़ियों को विभाजित करने की अनुमति देता है। इस नियम का क्या प्रभाव है?
मैं दिखाता हूँ कि अनंत पुनः-विभाजन का मूल्य, अधिकतम चार हाथों तक विभाजन की तुलना में, 0.05% है यदि यह नियम इक्कों सहित सभी जोड़ियों पर लागू होता है, और 0.02% है यदि इसमें इक्के शामिल नहीं हैं। यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फ़ोरम में उठाया गया था और इस पर चर्चा हुई थी।
जाहिर है, LVH के पास VCU के लिए 5000:1 के अनुपात में राष्ट्रीय चैंपियनशिप जीतने के लिए $10 का टिकट है। अगर VCU जीत जाता है, तो उसे $50,000 मिलेंगे। अगर आपके पास टिकट होता, तो इस समय आप कम से कम कितनी राशि स्वीकार करते? (अंतिम 4 कल से शुरू हो रहे हैं)
मैं देख रहा हूँ कि पिनेकल में VCU की चैंपियनशिप जीतने की संभावना इस प्रकार है: हाँ +604 नहीं -750 आइए जानें कि किसी भी तरह से बराबरी की जीत सुनिश्चित करने के लिए आपको VCU की जीत के खिलाफ कितना दांव लगाना होगा, और वह जीत कितनी होगी। मान लीजिए x दांव लगाता है। जीत का परिणाम = 50,000 - x
हार का परिणाम = x*(100/750) = (2/15)x इन्हें एक दूसरे के बराबर रखें 50000-x = (2/15)x 50000 = (17/15)xx = 50000×(15/17) x = $44,117.65 देखते हैं कि क्या यह सही है... अगर VCU जीतता है, तो परिणाम $50,000 घटाएँ हिल्टन से $44,117.65 घटाएँ पिनेकल को = $5,882.35 अगर VCU नहीं जीतता है, तो आपको हिल्टन से कुछ नहीं मिलेगा, लेकिन पिनेकल पर दांव $44,117.65 × (100/750) = $5,882.35 का होगा। हालाँकि, मुझे संदेह है कि VCU के खिलाफ दांव पर उचित ऑड्स मिलेंगे। अगर मालिक जोखिम से बेहद बचता है और टिकट बेचने के लिए उत्सुक है, तो मुझे लगता है कि लगभग 6,000 डॉलर उचित होंगे। हालाँकि, मैं VCU की जीत की संभावना +604 रेखा पर आधारित करूँगा, जिसका अर्थ है कि 100/704 = 14.2% संभावना। इससे टिकट का मूल्य लगभग 7,100 डॉलर हो जाएगा। यह सब कर संबंधी प्रभावों को नज़रअंदाज़ करता है। यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फ़ोरम में उठाया गया था और इस पर चर्चा हुई थी।
बैंकिंग न करते हुए पै गो पोकर में आपको सबसे अच्छा हाथ कौन सा मिल सकता है?
बैंकिंग के बिना कोई भी हाथ अपराजेय नहीं लगता। तो चलिए दो हाथों पर विचार करते हैं। पहला हाथ उच्च स्तर पर न तो हराया जा सकता है और न ही बराबरी पर। दूसरा हाथ निम्न स्तर पर न तो हराया जा सकता है और न ही बराबरी पर।
(1) AAAAW/KK (W=जंगली)
पाँच इक्कों को ऊँची बाजी में नहीं हराया जा सकता, लेकिन बादशाहों की जोड़ी को नीची बाजी में बराबर किया जा सकता है। दो बादशाहों के साथ संयोजनों की संख्या संयोजन (44,5) = 1,086,008 है। बचे 46 में से 7 पत्तों के कुल संयोजनों की संख्या 53,524,680 है। इसलिए दो बादशाहों की संभावना 1,086,008/53,524,680 = 2.03% है। इनमें से कई संयोजनों के साथ डीलर नीची बाजी में केके नहीं खेलेगा। मेरे पै गो पोकर परिशिष्ट 1 के अनुसार, डीलर के पास 74.93% समय ऊँची बाजी में इक्कों की जोड़ी या उससे कम होगी। इसका मतलब है कि वह दो जोड़ी या उससे बेहतर बनाएगा, जिससे वह नीची बाजी में, 25.07% समय राजाओं के साथ खेल सकेगा। अतः खिलाड़ी को दो राजा मिलने और उन्हें निम्न स्तर पर खेलने में सक्षम होने की संभावना 2.03% × 25.07% = 0.51%, या 196 में 1 है।
(2) AWQJT (सूटेड)/AA
रॉयल को हाई में टाई किया जा सकता है, लेकिन इक्के को लो में हराया या टाई नहीं किया जा सकता है। यहां मैं रॉयल बनाने के लिए किंग की जगह वाइल्ड का इस्तेमाल कर रहा हूं, लेकिन यह Q, J, या T की जगह भी आ सकता था। मैं नहीं चाहता कि यह इक्के की जगह ले, क्योंकि तब डीलर के पास लो को टाई करने के लिए डेक में दो इक्के बचेंगे। इस तरह, डीलर केवल एक और रॉयल के साथ हाई को टाई कर सकता है। इसकी संभावना क्या है? रॉयल के लिए तीन सूट बचे हैं, और अन्य दो कार्ड कुछ भी हो सकते हैं। इसलिए पुश करने वाले संयोजनों की संख्या 3×combin(41,2) = 2,460 है। खिलाड़ी द्वारा मूल 43 में से 7 हटाने के बाद डेक में बचे 46 कार्डों में से मुझे 41 मिलता है अतः वाइल्ड रॉयल/एए के साथ टाई होने की संभावना 2,460/53,524,680 = 0.004596%, या 21,758 में 1 है।
इससे पहले कि कोई परफेक्शनिस्ट मुझे लिखे, मैं बता दूँ कि कुछ अजीबोगरीब स्थितियाँ हो सकती हैं जहाँ डीलर उस तरह से हाथ नहीं खेलता जैसा मैं चाहता था। मैं हर स्थिति की सटीक संभावना जानने की कोशिश नहीं कर रहा हूँ, बल्कि यह साबित करना चाहता हूँ कि मुझे क्यों लगता है कि वाइल्ड रॉयल/AA, पै गो पोकर में बैंकिंग के बिना मिलने वाला सबसे अच्छा हाथ है।
यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फोरम में उठाया गया और इस पर चर्चा की गई।
समरूप जुड़वाँ के अलावा, मेरे किसी सगे भाई या बहन के साथ जीनों का कितना अनुपात समान होगा?
1/2.
अगर हम तुलना के लिए केनो का इस्तेमाल करें, तो हर व्यक्ति में 40 जीन होंगे, जिनमें से प्रत्येक एक केनो बॉल द्वारा दर्शाया जाएगा। हालाँकि, प्रत्येक बॉल का एक विशिष्ट नंबर होगा। जब दो लोग, जो आपस में संबंधित नहीं हैं, संभोग करते हैं, तो यह ऐसा है जैसे दोनों ने 80 गेंदों को एक हॉपर में मिला दिया हो, और संभोग से उत्पन्न संतानों के लिए यादृच्छिक रूप से 40 जीन चुन लिए हों।
तो जब आप गर्भवती हुईं, तो आपको हॉपर में आधी गेंदें मिलीं, और बाकी आधी बेकार हो गईं। जब आपके भाई या बहन का गर्भाधान हुआ, तो उन्हें आपके जन्म के समय निकाली गई गेंदों में से आधी मिलीं, और आधी जो नहीं निकाली गईं। तो आप आनुवंशिक रूप से 50% समान हैं। ठीक उसी तरह जैसे कि अगर केनो में 40 नंबर निकाले जाते हैं, तो दो लगातार निकाले गए नंबरों में औसतन 20 गेंदें समान होती हैं।
यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फोरम में उठाया गया और इस पर चर्चा की गई।
मेज और कुर्सियाँ बनाने वाली एक फैक्ट्री में 10 आरी, 6 खराद और 18 सैंडिंग मशीनें लगी हैं। एक कुर्सी को आरी पर 10 मिनट, खराद पर 5 मिनट और सैंडिंग में 5 मिनट लगते हैं। एक मेज को आरी पर 5 मिनट, खराद पर 5 मिनट और सैंडिंग में 20 मिनट लगते हैं। एक कुर्सी 10 डॉलर में और एक मेज 20 डॉलर में बिकती है। फैक्ट्री को प्रति घंटे कितनी मेज और कुर्सियाँ बनानी चाहिए ताकि उसे सबसे ज़्यादा राजस्व मिले, और वह राजस्व कितना है?
मान लीजिए कि c प्रति घंटे बनाई गई कुर्सियों की संख्या है और t मेज़ों की संख्या। प्रति घंटे राजस्व 10×c + 20×t होगा।
10 आरी चलाने से प्रति घंटे 600 मिनट आरी चलती है। हमें बताया गया था कि एक कुर्सी को आरी चलाने में 10 मिनट और एक मेज को 5 मिनट लगते हैं। इस प्रकार, प्रति घंटे उत्पादन की सीमा इस प्रकार है:
(1) 10c + 5t <= 600
6 खराद मशीनों से प्रति घंटे 360 मिनट खराद का काम होता है। हमें बताया गया था कि एक कुर्सी को आरी चलाने में 5 मिनट और एक मेज को 5 मिनट लगते हैं। इस प्रकार, प्रति घंटे उत्पादन की सीमा इस प्रकार है:
(2) 5c + 5t <= 360
18 सैंडिंग मशीनों से प्रति घंटे 1080 मिनट सैंडिंग होती है। हमें बताया गया था कि एक कुर्सी को आरी चलाने में 5 मिनट और एक मेज को 20 मिनट लगते हैं। इस प्रकार, प्रति घंटे उत्पादन की सीमा इस प्रकार है:
(3) 5c + 20t <= 1080
निम्नलिखित ग्राफ़ मशीनों के तीन सेटों द्वारा लगाई गई तीन बाधाओं को दर्शाता है। कारखाना कुर्सियों और मेज़ों के किसी भी संयोजन का उत्पादन कर सकता है जो तीनों रेखाओं के अंतर्गत आता है। प्रश्न यह है कि तीनों रेखाओं के अंतर्गत सबसे अधिक राजस्व कहाँ से प्राप्त होता है।
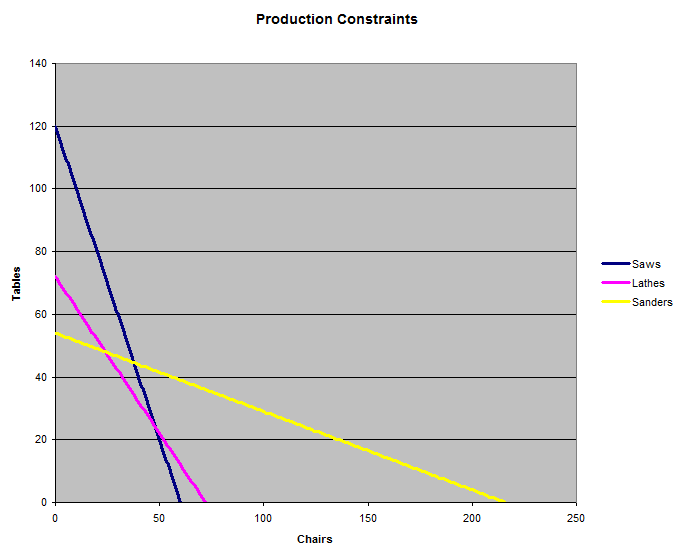
यह तर्कसंगत है कि उत्तर दो रेखाओं का प्रतिच्छेद बिंदु होगा, सभी कुर्सियाँ बनाएँ, या सभी मेज़ बनाएँ। तो आइए जानें कि रेखाएँ कहाँ प्रतिच्छेद करती हैं। सबसे पहले, आइए जानें कि समीकरण (1) और (2) कहाँ प्रतिच्छेद करते हैं। मशीनों का अधिकतम उपयोग करने के लिए हम <= व्यंजक को केवल = में बदल सकते हैं।
(1) 10c + 5t = 600
(2) 5c + 5t = 360
(1) में से (2) घटाएँ:
5सी = 240
सी = 48
समीकरण (1) में c के लिए 48 डालने पर:
10×48 + 5t = 600
5t = 120
टी = 24
अतः समीकरण (1) और (2) 48 कुर्सियों और 24 मेजों पर मिलते हैं।
अब, आइए जानें कि समीकरण (2) और (3) कहाँ मिलते हैं:
(2) 5c + 5t = 360
(3) 5c + 20t = 1080
(3) में से (2) घटाने पर:
15t = 720
टी = 48
इसे (2) या (3) में रखकर हम c का हल निकाल सकते हैं, जो 24 है।
अतः समीकरण (2) और (3) 24 कुर्सियों और 48 मेजों पर मिलते हैं।
हमें यह जानने की आवश्यकता नहीं है कि समीकरण (1) और (3) कहाँ मिलते हैं, क्योंकि हम ग्राफ से देख सकते हैं कि जहां आरी और सैंडर्स लाइनें मिलती हैं वह खराद बाधा के बाहर है।
यह भी संभव है कि केवल कुर्सियाँ बनाना ही सही उत्तर हो। ग्राफ़ दर्शाता है कि केवल कुर्सियाँ बनाने में आरी सबसे बड़ी बाधा है। समीकरण (1) से, यदि हम मेज़ों की संख्या के लिए 0 डालें, तो हमें c=60 प्राप्त होता है।
एक और संभावना केवल टेबल बनाने की है। ग्राफ़ दिखाता है कि सैंडर्स सबसे बड़ी सीमा होगी। समीकरण (3) में 0 कुर्सियाँ रखने पर, हम पाते हैं कि हम 54 से ज़्यादा टेबल नहीं बना सकते।
निम्नलिखित ग्राफ़ प्रत्येक व्यवहार्य उत्तर के लिए कुल राजस्व दर्शाता है। याद रखें, राजस्व प्रति कुर्सी $10 और प्रति मेज़ $20 है।
कुल प्रति घंटा राजस्व
| कुर्सियों | टेबल | आय |
| 0 | 54 | $1,080 |
| 24 | 48 | $1,200 |
| 48 | 24 | $960 |
| 60 | 0 | $600 |


