जादूगर से पूछो #265

आप माध्य और माध्यिका को लेकर भ्रमित हो रहे हैं। आइए, मेरी स्थिति को एक उदाहरण के रूप में देखें। मैं 45 वर्षीय पुरुष हूँ। मेरी जीवन प्रत्याशा 78.11 वर्ष है, फिर भी मेरे 80 वर्ष तक जीवित रहने की संभावना 50.04% है।

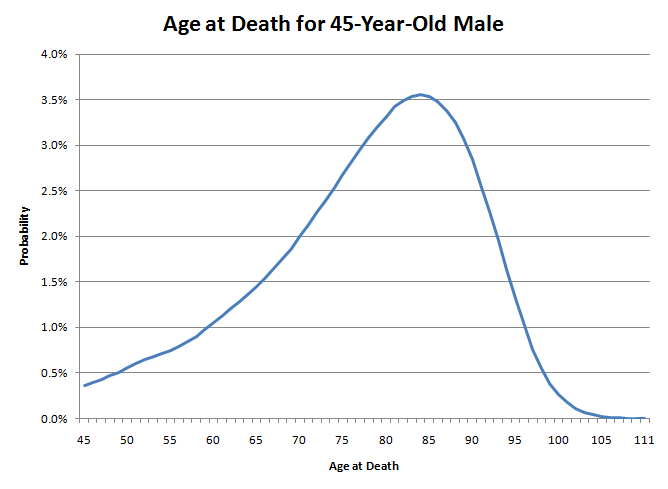
मेरी मृत्यु की आयु इस ग्राफ पर तीर चलाने जैसी होगी। ध्यान दें कि बायाँ भाग दाएँ भाग से कितना मोटा है। इसका मतलब है कि अभी मेरी मृत्यु की संभावना काफी कम है। हालाँकि, जैसे-जैसे मेरी उम्र बढ़ती जाएगी, अगले साल मृत्यु की संभावना और भी बढ़ती जाएगी। उदाहरण के लिए, एक 45 वर्षीय पुरुष के लिए 46 वर्ष तक जीवित रहने की संभावना 99.64% है, जो काफी अधिक है। हालाँकि, 85 वर्ष की आयु में 86 वर्ष तक जीवित रहने की संभावना केवल 89.21% है। यह ऐसा है जैसे प्रकृति धीरे-धीरे आपकी पीठ में छुरा घोंप रही हो। शुरुआत में शायद यह आपको नहीं मारेगी, लेकिन हर गुजरते साल के साथ, इसके होने की संभावना धीरे-धीरे बढ़ती जाती है। हालाँकि, जैसे-जैसे आप सत्तर के दशक के अंत में पहुँचते हैं, प्रकृति कहती है कि बहुत हो गया खेल और वास्तव में इसे अंदर धकेलना शुरू कर देती है।

इसलिए अगर 45 साल के बहुत से पुरुष इस ग्राफ़ पर तीर चलाएँ, तो 49.96% पुरुष 45 से 79 साल के बीच तीर चलाएँगे, और 50.04% पुरुष 80 से 111 साल के बीच तीर चलाएँगे। हालाँकि, ग्राफ़ के दाईं ओर आने वाले भाग्यशाली आधे पुरुष शायद 80 साल से ज़्यादा नहीं जी पाएँगे। एक बार जब कोई पुरुष 80 साल का हो जाता है, तो वह केवल 7.78 साल और जीने की उम्मीद कर सकता है। इस बीच, बदकिस्मत आधे पुरुषों में से कई, जो 80 साल तक नहीं पहुँच पाते, उससे भी कम उम्र में मर जाएँगे। इसलिए, कम उम्र में होने वाली मौतों की संख्या ही औसत जीवन प्रत्याशा को कम करती है।

इसी प्रकार की स्थिति के लिए, 10, 20, 30, 31, 32, 33 क्रमांक वाले पासे पर विचार करें। औसत 26 है, फिर भी इससे अधिक संख्या आने की 2/3 संभावना है।

माध्य और माध्यिका में अंतर को समझने के लिए, मान लीजिए कि हम नमूने में दो और मौतें जोड़ देते हैं। एक मौत 46 साल की उम्र में और एक 81 साल की उम्र में। 80 साल तक जीने की संभावना नहीं बदलती, लेकिन 45 साल की उम्र में औसत जीवन प्रत्याशा कम हो जाएगी।

यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फोरम में उठाया गया और इस पर चर्चा की गई।

अच्छा सवाल। हाउस वे कहते हैं कि पाँच इक्कों को बाँटकर, कम कीमत वाले हाथ में दो इक्के खेलें। अपवाद यह है कि अगर आप कम कीमत वाले हाथ में दो बादशाह खेल सकते हैं, तो उच्च कीमत वाले हाथ में एक तरह के पाँच इक्के ही रखें। मेरे पै गो पोकर पेज पर लास वेगास और अटलांटिक सिटी के सात हाउस वे बताए गए हैं, और उन सभी में यह अपवाद शामिल है। इन दो शहरों के बाहर के तीन इक्कों में यह अपवाद शामिल नहीं है।

चार इक्के, जोकर और दो बादशाह मिलने की संभावना 25,690,513 में से 1 है। यह मानते हुए कि डीलर बैंकिंग कर रहा है, यह अपवाद केवल तभी काम आएगा जब खिलाड़ी के पास हाई हैंड में एक तरह के चार या उससे बेहतर हों। इसकी संभावना लगभग 300 में से 1 है। दोनों के होने की संभावना लगभग 7.6 अरब में से 1 है।

नेवादा गेमिंग कंट्रोल बोर्ड के अनुसार, 2009 में नेवादा में 306 पै गो पोकर टेबल थे। यदि हम उदारतापूर्वक प्रति घंटे 60 हाथ, प्रति टेबल दो खिलाड़ी, और प्रत्येक टेबल 24/7 खुली रहती है, तो इस अपवाद को घटित होने और परिणाम में अंतर लाने में 23.7 वर्ष लगेंगे।

इसलिए कैसीनो हर पाई गो पोकर डीलर को यह अपवाद याद रखने के लिए बाध्य कर रहे हैं, जबकि खेल के इतिहास में इससे कभी कोई फ़र्क़ नहीं पड़ा होगा। मेरा अनुमान है कि जिस व्यक्ति ने यह नियम जोड़ने का विचार किया था, वही व्यक्ति यह भी तय कर रहा था कि A2345 स्ट्रेट, जिसे "व्हील" के नाम से जाना जाता है, दूसरा सबसे ऊँचा स्ट्रेट है।

प्रायिकता के क्षेत्र के इतिहास में यह एक क्लासिक समस्या है। कई लोग गलती से इसका उत्तर 18 मान लेते हैं, क्योंकि 12 आने की प्रायिकता 36 में 1 है, और 18×(1/36)=50% है। हालाँकि, इस तर्क से, 36 बार आने पर 12 आने की प्रायिकता 100% होगी, जो स्पष्ट रूप से नहीं है। यहाँ सही समाधान है। मान लीजिए r आने की संख्या है। 12 न आने की प्रायिकता 35/36 है। r आने पर 0 12 आने की प्रायिकता (35/36) ^r है। इसलिए हमें निम्नलिखित समीकरण में r का मान ज्ञात करना है:

(35/36) ^आर = 0.5
लॉग(35/36) ^आर = लॉग(0.5)
आर × लॉग(35/36) = लॉग(0.5)
आर = लॉग(0.5)/लॉग(35/36)
आर = 24.6051

तो इसका कोई गोल उत्तर नहीं है। 24 बार फेंकने पर 12 आने की प्रायिकता 1-(35/36) ²⁴ = 49.14% है। 25 बार फेंकने पर 12 आने की प्रायिकता 1-(35/36) ²⁵ = 50.55% है।

अगर आप इस पर दांव लगाना चाहते हैं, तो मान लीजिए कि आप 25 बार में 12 ला सकते हैं, या कोई और 24 बार में नहीं ला सकता। किसी भी तरह से आपको सम राशि पर फ़ायदा होगा।

मैं 10 से 1 का दांव लगाऊँगा, आपको भुगतान मिल जाएगा, हालाँकि वे पहले आपसे कुछ बातें कर सकते हैं। मुझे इसमें कुछ संदेह इसलिए है क्योंकि एक स्पोर्ट्स बुक, गेमिंग कंट्रोल बोर्ड की अनुमति से, स्पष्ट रूप से गलती से लगाए गए दांव को रद्द कर सकती है।

"कोई भी पुस्तक अध्यक्ष की पूर्व लिखित स्वीकृति के बिना किसी भी दांव को एकतरफा रद्द नहीं कर सकती।" - नेवादा विनियमन 22.115

हालाँकि यह अधिकार मौजूद है, लेकिन कुछ उदाहरणों के आधार पर, इसका इस्तेमाल बहुत कम होता है। मुझे बताइए क्या होता है।

पी.एस. मुझे बाद में प्रश्नकर्ता द्वारा सूचित किया गया कि उसे बिना किसी परेशानी के भुगतान कर दिया गया था।

हाँ, ऐसा होगा, e ^100,000 -1 सेकंड के बाद। दो समाधानों के लिए मेरी mathproblems.info साइट, समस्या 206 देखें।

यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फोरम में उठाया गया और इस पर चर्चा की गई।