जादूगर से पूछो #261
जैसे-जैसे सीज़न आगे बढ़ता है, मौसम खराब होता है, और टीमों के हालिया प्रदर्शन के बारे में ज़्यादा जानकारी मिलती है, फ़ुटबॉल के कुल योग पर सट्टेबाज़ी पर क्या प्रभाव पड़ता है? लाइन में गलतियाँ ढूँढ़ना कितना आसान (या मुश्किल) है?
इस प्रश्न का उत्तर देने में सहायता के लिए, मैंने 1983 से 2009 तक प्रत्येक सीज़न के आधार पर, एनएफएल में सप्ताह संख्या के आधार पर बनाए गए औसत अंकों का ग्राफ बनाया। निम्नलिखित ग्राफ परिणाम दर्शाता है।
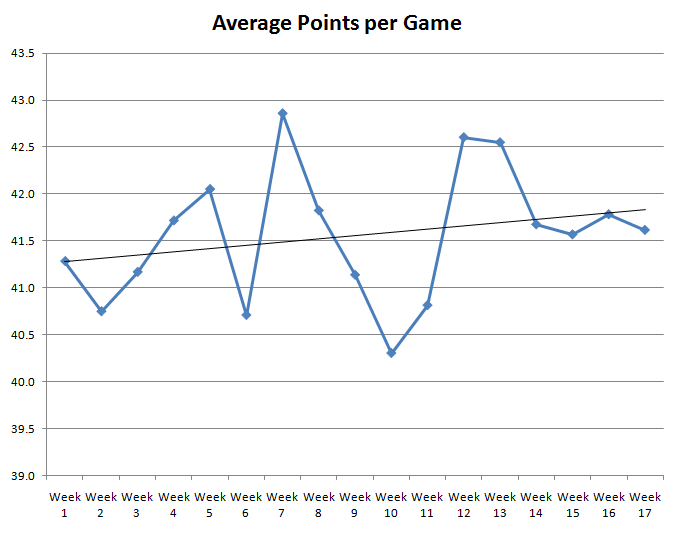
जैसा कि आप देख सकते हैं, रेखा बार-बार ऊपर-नीचे होती है। पतली काली रेखा एक न्यूनतम-वर्ग सर्वोत्तम फिट रेखा है, जो एक सामान्य ऊपर की ओर रुझान दर्शाती है। इसलिए जैसे-जैसे मौसम बदलता है और तापमान गिरता है, औसत अंक थोड़े बढ़ते हैं, लेकिन यह आसानी से एक यादृच्छिक बदलाव हो सकता है।
मैं बस इतना ही कह सकता हूँ। मौसम का खेल सट्टेबाजी पर क्या असर पड़ता है, इस बारे में सामान्य राय जानने के लिए मैंने अपने दोस्त जेसन बीन से बात की, जो इस विषय के विशेषज्ञ हैं। उन्होंने जो कहा, वह इस प्रकार है:
अधिकांश मामलों में, हवा मौसम का प्रमुख पहलू है जो खेल को सबसे अधिक प्रभावित करता है; लेकिन, यह एकमात्र नहीं है। बेसबॉल और अन्य आउटडोर खेलों में, छाया का समान प्रभाव हो सकता है, विशेष रूप से शुरुआती और बाद के सीज़न के बेसबॉल दोपहर के खेलों के दौरान। बारिश या बर्फ उतना बड़ा कारक नहीं है जितना कि ज्यादातर लोग फुटबॉल में सोचते हैं, क्योंकि यह आम तौर पर आक्रमण और रक्षा दोनों को समान रूप से प्रभावित करता है। एक उदाहरण एक विस्तृत रिसीवर के खिलाफ रक्षात्मक पीठ होगा। बारिश और बर्फ उन्हें समान रूप से धीमा कर देंगे, इस प्रकार किसी भी पक्ष को बढ़त नहीं मिलेगी। हवा किकिंग के साथ-साथ फुटबॉल में पासिंग गेम को भी खत्म कर सकती है। मैंने ऐसे खेल देखे हैं जहाँ एक पासिंग टीम को एक मजबूत क्रॉसविंड के कारण लगभग हर खेल में गेंद चलाने के लिए मजबूर होना पड़ा है।यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फोरम में उठाया गया और इस पर चर्चा की गई।
क्रेप्स में सामान्यतः क्या होता है, यदि कोई खिलाड़ी क्रेप्स में ऑड्स मल्टीपल से अधिक दांव लगाता है, तथा डीलर को तब तक इसका पता नहीं चलता, जब तक कि दांव जीत या हार नहीं जाता?
मैंने एक पूर्व टेबल वेगास गेम मैनेजर से इस बारे में पूछा। उन्होंने बताया कि लाइन बेट के अनुमत गुणक से ऊपर के ऑड्स बेट का हिस्सा प्लेस बेट ऑड्स पर भुगतान किया जाएगा। यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फ़ोरम में उठाया गया और इस पर चर्चा हुई।
एनएफएल में, औसतन, एक स्कोर के बाद दूसरी टीम द्वारा अगला स्कोर किये जाने की संभावना क्या होती है?
2000-2009 एनएफएल सीज़न के आधार पर, उत्तर 57% है।
एक ट्रूएल (तीन-तरफ़ा द्वंद्वयुद्ध) पर विचार करें जिसमें प्रतिभागी A, B और C शामिल हैं। वे एक महिला के लिए मरते दम तक लड़ रहे हैं। वे सभी सज्जन हैं, और वे सभी निम्नलिखित नियमों पर सहमत हैं।
- तीन प्रतिभागी एक त्रिकोण बनाते हैं।
- प्रत्येक के पास केवल एक गोली है।
- पहले A जाता है, फिर B, और फिर C।
- A के द्वारा किसी इच्छित लक्ष्य को भेदने की संभावना 10% है।
- B के इच्छित लक्ष्य को भेदने की संभावना 60% है।
- C के इच्छित लक्ष्य को भेदने की संभावना 90% है।
- कोई आकस्मिक गोलीबारी नहीं हुई है।
- हवा में गोली चलाना (जानबूझकर चूक जाना) और खुद को गोली मारना स्वीकार्य है, और ये हमेशा सफल होते हैं।
- अगर किसी भी राउंड के बाद दो या तीन लोग बच जाते हैं, तो हर एक को एक नई गोली दी जाती है। फिर वे बारी-बारी से उसी क्रम में गोली चलाएँगे, और पहले से मरे हुए लोगों को छोड़कर।
- तीनों प्रतिभागी उत्तम तर्कशास्त्री हैं।
A को शुरुआत में किस पर निशाना साधना चाहिए? हर शुरुआती लक्ष्य पर उसके बचने की संभावना क्या है?
इस पहेली पर बीबीसी के शो क्वाइट इंट्रेस्टिंग में चर्चा की गई है। उत्तर और समाधान के लिए 100 पंक्तियों तक नीचे स्क्रॉल करें।
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
प्रत्येक प्रारंभिक लक्ष्य के अनुसार A के जीतने की मेरी संभावनाएँ यहाँ दी गई हैं। जैसा कि आप देख सकते हैं, जानबूझकर हवा में गोली चलाने से A के जीतने की संभावना अधिकतम हो जाती है।
ट्रूएल ऑड्स
| रणनीति | संभवतः जीत |
| वायु | 13.887% |
| ए | 0.000% |
| बी | 12.560% |
| सी | 13.094% |
समाधान के लिए, आइए Pr(X) संकेतन का उपयोग करके समूह X के एक राउंड के बाद केवल समूह X के बचे रहने की प्रायिकता को दर्शाते हैं। आइए Pr(X*) शब्दावली का उपयोग करके समूह X के अंततः राउंड जीतने की प्रायिकता को दर्शाते हैं, जब तक कि किसी के चोटिल होने से खेल की स्थिति बदल न जाए। मान लीजिए Pr(X**) वह प्रायिकता है कि खिलाड़ी X अकेला जीवित बचेगा। अंतिम प्रायिकताएँ ज्ञात करने के लिए, आइए पहले दो खिलाड़ियों की स्थितियों पर नज़र डालें। यह स्पष्ट है कि प्रत्येक खिलाड़ी दूसरे पर गोली चलाएगा।
A बनाम B
- पीआर(ए) = 0.1
- पीआर(बी) = 0.9×0.6 = 0.54
- पीआर(एबी) = 0.9×0.4 = 0.36
अगर दोनों बच जाते हैं, तो ये तब तक दोहराए जाएँगे जब तक कि केवल एक ही जीवित न बचे। तो, अंतिम जीवित बचे व्यक्ति के होने की संभावनाएँ हैं:
- पीआर(ए*) = पीआर(ए)/(1-पीआर(एबी)) = 0.1/0.64 = 0.15625
- पीआर(बी*) = पीआर(बी)/(1-पीआर(एबी)) = 0.54/0.64 = 0.84375
A बनाम C
- पीआर(ए) = 0.1
- पीआर(सी) = 0.9×0.9 = 0.81
- पीआर(एसी) = 0.9×0.1 = 0.09
अगर दोनों बच जाते हैं, तो ये तब तक दोहराए जाएँगे जब तक कि केवल एक ही जीवित न बचे। तो, अंतिम जीवित बचे व्यक्ति के होने की संभावनाएँ हैं:
- पीआर(ए*) = पीआर(ए)/(1-पीआर(एसी)) = 0.1/0.91 = 0.10989011
- पीआर(सी*) = पीआर(बी)/(1-पीआर(एसी)) = 0.81/0.91= 0.89010989
बी बनाम सी
- पीआर(बी) = 0.6
- पीआर(सी) = 0.4×0.9 = 0.36
- पीआर(बीसी) = 0.$×0.1 = 0.04
अगर दोनों बच जाते हैं, तो ये तब तक दोहराए जाएँगे जब तक कि केवल एक ही जीवित न बचे। तो, अंतिम जीवित बचे व्यक्ति के होने की संभावनाएँ हैं:
- पीआर(बी*) = पीआर(ए)/(1-पीआर(बीसी)) = 0.6/.96 = 0.625
- पीआर(सी*) = पीआर(बी)/(1-पीआर(बीसी)) = 0.36/.96= 0.375
अब हम तीन खिलाड़ियों वाले मामले का विश्लेषण करने के लिए तैयार हैं। आइए उस स्थिति पर विचार करें जहाँ A, B पर निशाना साधता है।
तीन खिलाड़ी - A, B पर निशाना साधता है
अगर A, B से टकराता है, तो C निश्चित रूप से बच जाएगा, और A से टकरा भी सकता है और नहीं भी। इसलिए B से टकराने के दो संभावित परिणाम AC और C हैं। अगर A, B से चूक जाता है, तो B, बड़े खतरे C पर निशाना साधेगा। अगर B, C से टकराता है, तो A और B बच जाएँगे। अगर B, C से चूक जाता है, तो C, बड़े खतरे B पर निशाना साधेगा। अगर C, B से चूक जाता है, तो तीनों बच जाएँगे। अगर C, B से टकराता है, तो A और C बच जाएँगे। इसलिए संभावित परिणाम C, AB, AC और ABC हैं।
- पीआर(ए) = 0.
- पीआर(बी) = 0.
- Pr(C) = 0.1 × 0.9 = 0.09. यह A द्वारा B को और फिर C द्वारा A को मारने पर प्राप्त होता है।
- Pr(AB) = 0.9 × 0.6 = 0.54. यह तब प्राप्त होता है जब A, B को चूक जाता है, और फिर B, C से टकराता है।
- Pr(AC) = 0.1 × 0.1 + 0.9 × 0.4 × 0.9 = 0.334। इसे दो तरीकों से प्राप्त किया जा सकता है। पहला, A, B से टकराता है और फिर C, A से चूक जाता है। दूसरा, A, B से चूक जाता है, B, C से चूक जाता है और फिर C, B से टकराता है।
- पीआर(बीसी) = 0.
- Pr(ABC) = 0.9 × 0.4 × 0.1 = 0.036. यह तीनों लुप्त संख्याओं द्वारा प्राप्त होता है।
दो खिलाड़ियों वाले मामलों के समान तर्क से, हम प्रत्येक स्थिति की संभावनाओं को ज्ञात करने के लिए प्रत्येक परिणाम को (1-Pr(ABC))=0.964 से विभाजित कर सकते हैं, यह मानते हुए कि राउंड के बाद खेल की स्थिति बदल गई।
- पीआर(सी*) = 0.09/0.964 = 0.093361।
- पीआर(एबी*) = 0.54/0.964 = 0.560166।
- पीआर(एसी*) = 0.334/0.964 = 0.346473।
दो खिलाड़ियों वाले मामले से, हम जानते हैं कि अगर A और B की स्थिति आती है, तो A की जीत की संभावना 0.15625 और B की 0.84375 होगी। अगर A और C की स्थिति आती है, तो A की जीत की संभावना 0.109890 और C की 0.890110 होगी।
- Pr(A**) = (0.560165975 × 0.15625) + (0.346473029 × 0.10989011) = 0.125600. A दो तरीकों से विजेता हो सकता है: (1) AB अवस्था में पहुँचकर, और फिर जीत हासिल करके, या (2) AC अवस्था में पहुँचकर और फिर जीत हासिल करके।
- Pr(B**) = 0.560166 × 0.84375 = 0.472640. यदि B, AB अवस्था में पहुँच जाता है, तो वह विजेता होगा, और तब B जीत जाएगा।
- Pr(C**) = 0.093361 + (0.346473 × 0.890110) = 0.401760. C जीत सकता है यदि A, B को मार दे, और फिर C पहले राउंड में A को मार दे, या फिर वह AC अवस्था में पहुँच जाए, और फिर C जीत जाए।
इसलिए, यदि A की रणनीति सबसे पहले B पर निशाना साधने की है, तो उसके अकेले जीवित बचे रहने की संभावना 12.56% है।
तीन खिलाड़ी - A, C पर निशाना साधता है
अगर A, C से टकराता है, तो B निश्चित रूप से बच जाएगा, और A से टकरा भी सकता है और नहीं भी। इसलिए C से टकराने के दो संभावित परिणाम AB और B हैं। अगर A, C से चूक जाता है, तो B, बड़े खतरे C पर निशाना लगाएगा। अगर B, C से टकराता है, तो A और B बच जाएँगे। अगर B, C से चूक जाता है, तो C, बड़े खतरे B पर निशाना लगाएगा। अगर C, B से चूक जाता है, तो तीनों बच जाएँगे। अगर C, B से टकराता है, तो A और C बच जाएँगे। इसलिए संभावित परिणाम B, AB, AC और ABC हैं।
- पीआर(ए) = 0.
- पीआर(बी) = 0.1 × 0.6 = 0.06.
- पीआर(सी) = 0.
- Pr(AB) = (0.1 × 0.4) + (0.9 × 0.6) = 0.04+0.54 = 0.58. इसे दो तरीकों से प्राप्त किया जा सकता है।पहला है A, C को मारता है, और फिर B, A को चूक जाता है। दूसरा है A, B को चूक जाता है, और फिर B, C को मारता है।
- Pr(AC) = 0.9 × 0.4 × 0.9 = 0.324. यह A द्वारा C को खो देने, B द्वारा C को खो देने और C द्वारा B को मार देने पर प्राप्त होता है।
- पीआर(बीसी) = 0.
- Pr(ABC) = 0.9 × 0.4 × 0.1 = 0.036. यह तीनों लुप्त संख्याओं द्वारा प्राप्त होता है।
दो खिलाड़ियों वाले मामलों के समान तर्क से, हम प्रत्येक स्थिति की संभावनाओं को ज्ञात करने के लिए प्रत्येक परिणाम को (1-Pr(ABC))=0.964 से विभाजित कर सकते हैं, यह मानते हुए कि राउंड के बाद खेल की स्थिति बदल गई।
- पीआर(बी*) = 0.06/0.964 = 0.062241।
- पीआर(एबी*) = 0.58/0.964 = 0.601660।
- पीआर(एसी*) = 0.324/0.964 = 0.336100।
ए मामले के समाधान के समान तर्क से बी मामले को लक्ष्य बनाया गया है:
- पीआर(ए**) = (0.601660 × 0.15625) + (0.336100 × 0.10989011) = 0.130943।
- पीआर(बी**) = 0.062241 + 0.601660 × 0.84375 = 0.569891।
- पीआर(सी**) = 0.336100 × 0.890110 = 0.299166।
इसलिए, यदि A की रणनीति पहले C पर निशाना साधने की है, तो उसके अकेले जीवित बचे रहने की संभावना 13.09% है।
तीन खिलाड़ी - A जानबूझकर चूक जाता है
A के जानबूझकर चूकने पर B, बड़े खतरे C पर निशाना लगाएगा। अगर B, C को मारता है, तो A और B बच जाएँगे। अगर B, C को चूक जाता है, तो C, बड़े खतरे B पर निशाना लगाएगा। अगर C, B को चूक जाता है, तो तीनों बच जाएँगे। अगर C, B को मारता है, तो A और C बच जाएँगे। इसलिए संभावित परिणाम AB, AC और ABC हैं।
- पीआर(ए) = 0.
- पीआर(बी) = 0.
- पीआर(सी) = 0.
- Pr(AB) = 0.6. यह B द्वारा C पर प्रहार करने पर प्राप्त होता है।
- Pr(AC) = 0.4 × 0.9 = 0.36. यह तब प्राप्त होता है जब B, C से चूक जाता है, और फिर C, B से टकराता है।
- पीआर(बीसी) = 0.
- Pr(ABC) = 0.4 × 0.1 = 0.04. यह तीनों लुप्त संख्याओं द्वारा प्राप्त होता है।
दो खिलाड़ियों वाले मामलों के समान तर्क से, हम प्रत्येक स्थिति की संभावनाओं को ज्ञात करने के लिए प्रत्येक परिणाम को (1-Pr(ABC))=0.96 से विभाजित कर सकते हैं, यह मानते हुए कि राउंड के बाद खेल की स्थिति बदल गई।
- पीआर(एबी*) = 0.6/0.96 = 0.625.
- पीआर(एसी*) = 0.36/0.96 = 0.375.
ए मामले के समाधान के समान तर्क से बी मामले को लक्ष्य बनाया गया है:
- पीआर(ए**) = (0.625 × 0.15625) + (0.375 × 0.109890) = 0.138865।
- पीआर(बी**) = 0.625 × 0.84375 = 0.527344।
- पीआर(सी**) = 0.375 × 0.890110 = 0.333791।
इसलिए, यदि A की रणनीति पहले C पर निशाना साधने की है, तो उसके अकेले जीवित बचे रहने की संभावना 13.89% है।
यह प्रश्न मेरी सहयोगी साइट विज़ार्ड ऑफ़ वेगास के फोरम में उठाया गया और इस पर चर्चा की गई।


