जादूगर से पूछो #229

किसी कैसीनो को बड़े खिलाड़ियों से होने वाले वित्तीय जोखिम को सीमित करने के लिए आप किस तरह के अधिकतम दांव की सलाह देंगे? मुझे ब्लैकजैक के गणितीय घरेलू लाभ के बारे में पता है, लेकिन इससे यह तथ्य नहीं बदलता कि अगर सीमाएँ बहुत ऊँची हों, तो एक बड़ा खिलाड़ी कैसीनो को आसानी से गंभीर नुकसान पहुँचा सकता है।

Frank से Copenhagen

अगर मैं एक कैसीनो चलाता, तो मैं अधिकतम दांव तय करने के लिए केली मानदंड लागू करता। मैं सभी खेलों के लिए m*v/h को बराबर करता, जहाँ m अधिकतम दांव है, v विचरण है, और h हाउस एज है। इसे जोखिम भागफल कहते हैं। उदाहरण के लिए, मान लीजिए कि मैं बैकारेट में बैंकर बेट पर $150,000 लगाने में सहज हूँ, जो लगभग उतना ही है जितना एक बड़ा स्ट्रिप कैसीनो लेगा। हाउस एज 1.06% है, और विचरण 0.93· ² है। इस प्रकार जोखिम भागफल 150,000*0.93 ^·2 /0.0106 = 12,239,150 है।

अब, ब्लैकजैक में जोखिम भागफल को बराबर करने के लिए m का मान हल करें। उदार स्ट्रिप नियमों के साथ, हाउस एज 0.29% है। मान लीजिए कि खिलाड़ी तीन स्पॉट तक दांव लगा सकता है। तीन दांव स्पॉट दिए जाने पर, प्रति हाथ मानक विचलन 1.51957 है, इसलिए विचरण 1.51957 ^{· 2} = 2.3091 है। m का मान हल करने पर...

एम×2.3091/0.0029 = 12,239,150
मी = $15,371.

व्यावहारिक रूप से, बहुत कम खिलाड़ी परफेक्ट बेसिक स्ट्रैटेजी खेलते हैं, इसलिए मैं इसे बढ़ाकर $20,000 कर सकता हूँ। बड़े स्ट्रिप कैसीनो ब्लैकजैक में लगभग इतनी ही रकम लेंगे, इसलिए मुझे लगता है कि इसमें समानता है। मुझे लगता है कि नए खेलों में उन्हें बड़े दांव लगाने चाहिए।

मैं ऑनलाइन पोकर के एक खेल में शामिल था और ऐसा होने की संभावना जानना चाहता हूँ, कृपया:

David T. से Montego Bay

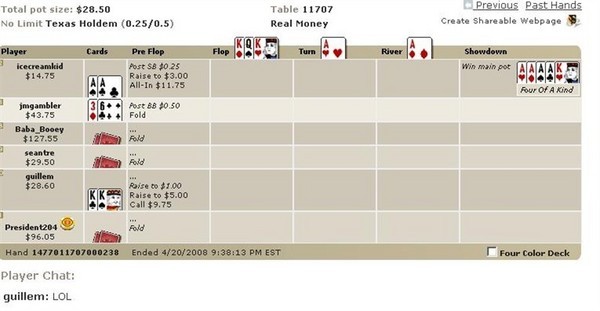
आम तौर पर मैं खराब बीट वाले सवालों से तंग आ जाता हूँ, लेकिन इस सवाल को नज़रअंदाज़ करना बहुत मुश्किल था। पहला पत्ता बंटने से पहले, दो खिलाड़ियों वाले खेल में, जिसमें दोनों खिलाड़ियों के पास पॉकेट पेयर हों, चार बादशाहों के चार इक्कों से हारने की प्रायिकता 2* कॉम्बिन (4,2)*कॉम्बिन(4,2)*44/(कॉम्बिन(52,2)*कॉम्बिन(50,2)*कॉम्बिन(48,5)) = 2*6*6*44/(1326*1225*1712304) = 877,961,175 में 1 है। यह छह खिलाड़ियों वाला खेल था, इसलिए कॉम्बिन(6,2) = 15 अलग-अलग खिलाड़ियों के जोड़े हैं। छह खिलाड़ियों वाले खेल में, यह प्रायिकता 15 गुना ज़्यादा है, यानी 58,530,745 में 1। संकेतित होल कार्ड बांटे जाने के बाद, तथा फ्लॉप से पहले, संभावना 38,916 में 1 है कि हाथ वैसे ही समाप्त होगा जैसा हुआ था।

आपकी पै गो (टाइल्स) रणनीतियाँ फॉक्सवुड्स हाउस वे के लिए अनुकूलित हैं, जो फरवरी 1997 में जारी किया गया था। आपकी कुछ रणनीतियों में, खिलाड़ी की बढ़त या लगभग सम ऑड्स दिखाई देते हैं। क्या आपको पता है कि वेगास या अन्य जगहों के किसी कैसिनो ने आपकी वेबसाइट पढ़ी है और अपने हाउस वे को उसके अनुसार समायोजित किया है? क्या आपके पास विभिन्न कैसिनो के हाउस वे के बारे में कोई और अद्यतन जानकारी है? इसके अलावा, पै गो के लिए आपकी ऑड्स तालिका में, आपके पास एक "इष्टतम" रणनीति है, लेकिन मुझे यह स्पष्ट नहीं है कि उस रणनीति के नियम कहाँ हैं। "इष्टतम" रणनीति क्या है? मैं वास्तव में खेल का आनंद ले रहा हूँ, और इसे पूरा करने, मज़े करने और बिना ज़्यादा पैसा गँवाए कॉम्प्स पाने के तरीके खोज रहा हूँ।

गुमनाम

वेगास में सीज़र्स पैलेस ने पिछले कुछ सालों में अपना हाउस वे बदल दिया है। पहले, वे कभी भी जी जून पेयर को अलग नहीं करते थे, और अब करते हैं। मैंडले बे के एक डीलर ने हाल ही में मुझे 3-4 के बजाय 0-7 खेलने के नियम में बदलाव के बारे में बताया। इन बदलावों के पीछे की वजह के बारे में, मुझे कुछ नहीं पता। अगर मेरा इसमें कोई हाथ होता, तो मुझे गर्व होता।

मैंने हाल ही में कैसिनो कैनबरा के लिए एक हाउस वे जोड़ा है। भविष्य में मैं अटलांटिक सिटी के क्लेरिज और लास वेगास के ट्रेजर आइलैंड के लिए भी हाउस वे जोड़ सकता हूँ। इन्हें HTML में डालना बहुत थकाऊ और समय लेने वाला है, इसलिए मैंने अभी तक ऐसा नहीं किया है।

मेरे सहायक जेबी फॉक्सवुड्स हाउस के रास्ते के खिलाफ एक बेहतरीन रणनीति पर काम कर रहे हैं। यह जल्द ही साइट पर आ जाएगी।

वन-कार्ड पोकर के खेल में तीन पत्तों का डेक होता है, जिसमें एक इक्का, एक ड्यूस और एक ट्रे होता है। इक्का सबसे छोटा और एक ट्रे सबसे बड़ा होता है। दो खिलाड़ी पॉट में $1 डालते हैं। फिर, प्रत्येक खिलाड़ी को एक पत्ता मिलता है। दांव लगाने का क्रम पहले से तय होता है, जिसमें खिलाड़ी 1 पहले दांव लगाता है। खिलाड़ी 1 या तो $1 का दांव लगा सकता है या चेक लगा सकता है। यदि खिलाड़ी 1 दांव लगाता है, तो खिलाड़ी 2 या तो कॉल कर सकता है या फोल्ड कर सकता है। यदि खिलाड़ी 1 चेक करता है, तो खिलाड़ी 2 या तो $1 का दांव लगा सकता है या चेक लगा सकता है। यदि खिलाड़ी 1 चेक करता है, और खिलाड़ी 2 दांव लगाता है, तो खिलाड़ी 1 या तो कॉल कर सकता है या फोल्ड कर सकता है। यदि दोनों खिलाड़ी चेक करते हैं, या दोनों दांव लगाते हैं, तो बड़ा पत्ता पॉट जीत जाता है। यह मानते हुए कि दोनों खिलाड़ी पूर्ण तर्कशास्त्री हैं, प्रत्येक खिलाड़ी के लिए सर्वोत्तम रणनीति क्या है?

Victor M. से Genoa City, WI

मुझे उम्मीद है आप खुश होंगे; मैंने इस पर पूरा दिन लगा दिया। इसका उत्तर और समाधान मेरी दूसरी साइट mathproblems.info , समस्या 203, या जेसन स्वानसन द्वारा लिखे गए अकादमिक पेपर "गेम थ्योरी एंड पोकर" पर मिल सकता है।