जादूगर से पूछो #227
तीन साल पहले, " आस्क द विज़ार्ड" कॉलम में, आपने लिखा था: "आप सही कह रहे हैं कि पासों को प्रभावित करने के पक्ष या विपक्ष में 500 पासे बहुत कम हैं, लेकिन 500 पासे फेंकना शून्य से बेहतर है।" क्या आप बता सकते हैं कि किसी प्रयोग में, किसी कथित पासा प्रभावित करने वाले से आपको क्या अपेक्षा करनी होगी, ताकि आप उस पर अच्छी-खासी रकम दांव पर लगाने के लिए पर्याप्त आश्वस्त हो सकें? मैं इसलिए पूछ रहा हूँ क्योंकि कुछ ब्लैकजैक सिम्स में "विश्वसनीय" परिणामों के लिए एक अरब पासे एक अच्छा मानक हैं। सबसे कुशल (अर्थात कम से कम पासे फेंकने वाले) प्रायोगिक डिज़ाइन के साथ, शूटर को परिणामों को प्रभावित करने का भरोसा दिलाने के लिए कितने पासे फेंकने होंगे? मुझे पता है कि जवाब शूटर के कौशल पर निर्भर करेगा, लेकिन आप मेरी बात समझ रहे होंगे। अगर आपको सबसे अच्छी स्थिति में भी दस लाख पासे फेंकने की ज़रूरत है, तो यह कोई सार्थक प्रयास नहीं होगा।
आत्मविश्वास अर्जित करने का कोई निश्चित बिंदु नहीं है। यह डिग्री का मामला है। सबसे पहले, मैं पूछूँगा कि किस चीज़ के लिए परीक्षण किया जा रहा है, और निशानेबाज़ का अनुमान क्या होगा। किसी भी परीक्षण में दो संभावित त्रुटियाँ होती हैं। एक कुशल निशानेबाज़ दुर्भाग्य के कारण असफल हो सकता है, या कोई यादृच्छिक निशानेबाज़ अच्छे भाग्य के कारण उत्तीर्ण हो सकता है। इन दोनों में से, मैं गलत सकारात्मक परिणाम से बचना पसंद करूँगा। मुझे लगता है कि एक उचित परीक्षण में गलत नकारात्मक परिणाम की संभावना लगभग 5% और गलत सकारात्मक परिणाम की संभावना लगभग 1% निर्धारित की जाएगी।
उदाहरण के लिए, मान लीजिए दावेदार कहता है कि वह पासों को हर सात बार फेंकने पर औसतन एक सात का योग प्राप्त कर सकता है। एक यादृच्छिक निशानेबाज औसतन हर छह बार फेंकने पर एक सात फेंकेगा। परीक्षण और त्रुटि के आधार पर, मुझे पता चला है कि इन दोनों मानदंडों को पूरा करने वाला एक परीक्षण 3,600 बार पासे फेंकने और पास होने के लिए 547 या उससे कम सात की आवश्यकता होगी, या 6.58 बार फेंकने पर एक सात।
सात में से एक निशानेबाज़ को औसतन 514.3 सात फेंकने चाहिए, जिसका मानक विचलन 21.00 है। गॉसियन सन्निकटन का उपयोग करते हुए, ऐसे कुशल निशानेबाज़ द्वारा 548 या अधिक सात फेंकने की संभावना (एक मिथ्या नकारात्मक) 5.7% है। एक यादृच्छिक निशानेबाज़ को औसतन 600 सात फेंकने चाहिए, जिसका मानक विचलन 22.36 है। एक यादृच्छिक निशानेबाज़ के परीक्षण में उत्तीर्ण होने की संभावना (एक मिथ्या सकारात्मक) 0.94% है। नीचे दिया गया ग्राफ़ कुशल और यादृच्छिक निशानेबाज़ों के संभावित परिणाम दर्शाता है। यदि परिणाम हरी रेखा के बाईं ओर हैं, तो मैं मान लूँगा कि निशानेबाज़ ने परीक्षण पास कर लिया है, और मैं उस पर दांव लगाऊँगा।
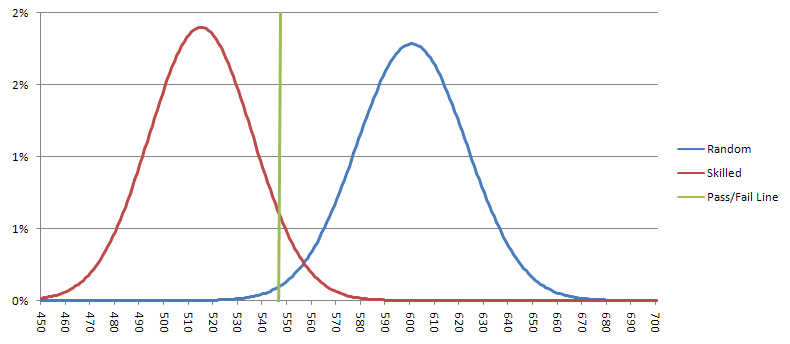
व्यावहारिक दुविधा यह है कि अगर हम प्रति मिनट दो थ्रो मान लें, तो परीक्षण करने में 30 घंटे लगेंगे। शायद मैं समय की आवश्यकता को कम करने के लिए महत्व के स्तर के बारे में अधिक उदार हो सकता था, लेकिन परिणाम उतने विश्वसनीय नहीं होंगे। मुझे लगता है कि 500-रोल वोंग प्रयोग से भी बड़े परीक्षण का समय आ गया है।
अगर लकी लेडी साइड बेट सिर्फ़ तभी खेला जाए जब ट्रू काउंट, मान लीजिए, 10 या उससे ज़्यादा हो, तो क्या कोई हाउस एज को हरा पाएगा? अगर हाँ, तो इस साइड बेट में हाउस एज को हराने के लिए न्यूनतम ट्रू काउंट क्या है?
मैंने खुद उस दांव पर कार्ड गिनने के असर का अध्ययन नहीं किया है। हालाँकि, अर्नोल्ड स्नाइडर ने किया है, और उनके नतीजे उनकी "बिग बुक ऑफ़ ब्लैकजैक" में पाए जा सकते हैं। वहाँ वे कहते हैं कि अगर छह डेक वाले खेल में आखिरी दो डेक हैं और गिनती +10 या उससे ज़्यादा है, तो आपको रेड सेवन्स काउंट का इस्तेमाल करके दांव लगाना चाहिए। डबल-डेक वाले खेल में, वे आखिरी डेक पर दांव लगाने और +6 या उससे ज़्यादा की गिनती होने की सलाह देते हैं।
जब हाउस 6-डेक शू पर लेट सरेंडर की अनुमति देता है, जब हाउस सॉफ्ट 17 पर पहुँच जाता है, और जब हाउस सॉफ्ट 17 पर खड़ा रहता है, तो खिलाड़ी को क्या लाभ होता है? 8-डेक शू के बारे में क्या?
इस तरह के सवालों के जवाब मेरे हाउस-एज कैलकुलेटर का इस्तेमाल करके, एक नियम बदलकर और हाउस एज पर पड़ने वाले असर को देखकर मिल सकते हैं। आमतौर पर मैं आपको ऐसा करने के लिए कहता, लेकिन आज मैं धैर्य रखने के मूड में हूँ, तो लीजिए:
6 डेक, डीलर सॉफ्ट 17 पर खड़ा है: 0.0726%
8 डेक, डीलर सॉफ्ट 17 पर खड़ा है: 0.0758%
6 डेक, डीलर सॉफ्ट 17 पर हिट करता है: 0.0882%
8 डेक, डीलर सॉफ्ट 17 पर हिट करता है: 0.0916%
मैं सोच रहा था कि क्या कोई ऐसा तरीका है जिससे यह गणना की जा सके कि बैकारेट में खिलाड़ी पर दांव लगाते समय किसी भी बिंदु से दस यूनिट खोने के लिए औसतन कितने प्रयास करने होंगे।
आठ डेक मानकर, खिलाड़ी के दांव पर हाउस एज 1.2351% है। दस इकाइयों का नुकसान होने के लिए अपेक्षित हाथों की संख्या 10/0.012351 = 809.66 है।
मैं हाल ही में अपने परिवार के कुछ सदस्यों के साथ एक घरेलू पोकर खेल (ओमाहा ड्यूसेस वाइल्ड) खेल रहा था। पाँच खिलाड़ी थे, और अब दो ही बचे थे। मैं उन दो में से एक था। दूसरा खिलाड़ी पूरी रात जीतता रहा था। आखिरकार मेरे पास एक अच्छा हाथ था। मैंने उसकी तरफ देखा और मज़ाकिया अंदाज़ में "चार सेवन" कहा। उसने कहा कि उसके पास चार इक्के हैं, और चिप्स रेक करने लगी। फिर मैंने खुद को सुधारा, और बताया कि मेरे पास स्ट्रेट फ्लश है। फिर उसने मुझे बताया कि मैंने पहले ही चार सेवन कॉल कर लिए हैं। मैंने अपना हाथ दिखाया और वह फिर भी ज़ोर देकर कहती रही कि मैंने पहले ही चार सेवन कॉल कर लिए हैं, और मेरा हाथ अब अच्छा नहीं रहा। तो सवाल यह है कि हाथ किसने जीता? ज़ाहिर है कि स्ट्रेट फ्लश, एक तरह के चार को मात देता है। लेकिन क्या मैंने जो कहा, उससे मैंने अपना हाथ खराब कर लिया? पैसा अभी भी मेज पर है।
आखिरकार, पत्ते ही बोलते हैं। तुम्हें वह हाथ जीतना चाहिए था।


